Trên đường tròn tâm $S_{1}$ có bao nhiêu điểm cực tiểu?

hoankuty đã viết:

Bài toán
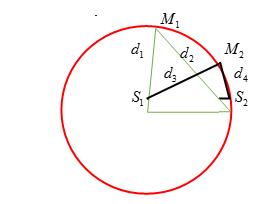
Cho hai nguồn sóng kết hợp đồng pha $S_{1}$ và $S_{2}$ tạo ra hệ giao thoa sóng trên mặt nước. Xét đường tròn tâm $S_{1}$ bán kính $S_{1}S_{2}$ ,$M_{1}$ và $M_{2}$ lần lượt là các cực đại giao thoa nằm trên đường tròn, xa $S_{2}$ nhất và gần $S_{2}$ nhất. Biết $M_{1}S_{2}-M_{2}S_{2}=12\left(cm\right);S_{1}S_{2}=10\left(cm\right)$. Trên đường tròn tâm $S_{1}$ có bao nhiêu điểm cực tiểu?
A. 4
B. 6
C. 8
D. 10

Click để xem thêm...

Lời giải
Ta có: $\begin{cases} & \text S_1M_1-S_2M_1=-k\lambda \\ & \text S_1M_2-S_2M_2=k\lambda \end{cases}$ với $S_1M_1=S_1M_2=S_1S_2=10 \left(cm\right)$
$\Rightarrow S_2M_1-S_2M_2=2k\lambda \Rightarrow k\lambda =6\left(cm\right)$
Với: $k=[\dfrac{10}{\lambda}]$ (Lấy phần nguyên) $\Rightarrow [\dfrac{10}{\lambda}]\lambda =6\left(1\right)$
Thử với $\lambda \in N$ từ $1\left(cm\right)\rightarrow 6\left(cm\right):$ thỏa (1)
$\Rightarrow $ Số đường cực tiểu: $N_t=2[\dfrac{10}{6}+\dfrac{1}{2}]=4$
Bài này lại có hai đáp án: theo cách thứ 2:
$\begin{array}{l}\left\{ \begin{array}{l}{d_2} - {d_1} = k\lambda \\{d_3} - {d_4} = k\lambda \end{array} \right. \Rightarrow {d_3} - {d_4} + {d_2} - {d_1} = 2k\lambda \Rightarrow k\lambda = 6 \Rightarrow \lambda = \dfrac{6}{k}\\ \bullet k = 1 \Rightarrow \lambda = 6 \Rightarrow \dfrac{{AB}}{\lambda } = 1,666 \Rightarrow 4CT\\ \bullet k = 2 \Rightarrow \lambda = 3 \Rightarrow \dfrac{{AB}}{3} = 3,333 \Rightarrow 6CT\end{array}$
Hình vẽ

datanhlg đã viết:

Lời giải
Ta có: $\begin{cases} & \text S_1M_1-S_2M_1=-k\lambda \\ & \text S_1M_2-S_2M_2=k\lambda \end{cases}$ với $S_1M_1=S_1M_2=S_1S_2=10 \left(cm\right)$
$\Rightarrow S_2M_1-S_2M_2=2k\lambda \Rightarrow k\lambda =6\left(cm\right)$
Với: $k=[\dfrac{10}{\lambda}]$ (Lấy phần nguyên) $\Rightarrow [\dfrac{10}{\lambda}]\lambda =6\left(1\right)$
Thử với $\lambda \in N$ từ $1\left(cm\right)\rightarrow 6\left(cm\right):$ thỏa (1)
$\Rightarrow $ Số đường cực tiểu: $N_t=2[\dfrac{10}{6}+\dfrac{1}{2}]=4$
Bài này lại có hai đáp án: theo cách thứ 2:
$\begin{array}{l}\left\{ \begin{array}{l}{d_2} - {d_1} = k\lambda \\{d_3} - {d_4} = k\lambda \end{array} \right. \Rightarrow {d_3} - {d_4} + {d_2} - {d_1} = 2k\lambda \Rightarrow k\lambda = 6 \Rightarrow \lambda = \dfrac{6}{k}\\ \bullet k = 1 \Rightarrow \lambda = 6 \Rightarrow \dfrac{{AB}}{\lambda } = 1,666 \Rightarrow 4CT\\ \bullet k = 2 \Rightarrow \lambda = 3 \Rightarrow \dfrac{{AB}}{3} = 3,333 \Rightarrow 6CT\end{array}$
Hình vẽ

Click để xem thêm...

Đề bài hỏi điểm cực tiểu trên đường tròn mà anh. Cứ lấy hạnh phúc nhân đôi là đánh lụi được đáp án mà :)

hoankuty đã viết:

Đề bài hỏi điểm cực tiểu trên đường tròn mà anh. Cứ lấy hạnh phúc nhân đôi là đánh lụi được đáp án mà :)

Click để xem thêm...

Thế đáp án là bao nhiêu vậy cậu?

datanhlg đã viết:

Lời giải
Ta có: $\begin{cases} & \text S_1M_1-S_2M_1=-k\lambda \\ & \text S_1M_2-S_2M_2=k\lambda \end{cases}$ với $S_1M_1=S_1M_2=S_1S_2=10 \left(cm\right)$
$\Rightarrow S_2M_1-S_2M_2=2k\lambda \Rightarrow k\lambda =6\left(cm\right)$
Với: $k=[\dfrac{10}{\lambda}]$ (Lấy phần nguyên) $\Rightarrow [\dfrac{10}{\lambda}]\lambda =6\left(1\right)$
Thử với $\lambda \in N$ từ $1\left(cm\right)\rightarrow 6\left(cm\right):$ thỏa (1)
$\Rightarrow $ Số đường cực tiểu: $N_t=2[\dfrac{10}{6}+\dfrac{1}{2}]=4$
Bài này lại có hai đáp án: theo cách thứ 2:
$\begin{array}{l}\left\{ \begin{array}{l}{d_2} - {d_1} = k\lambda \\{d_3} - {d_4} = k\lambda \end{array} \right. \Rightarrow {d_3} - {d_4} + {d_2} - {d_1} = 2k\lambda \Rightarrow k\lambda = 6 \Rightarrow \lambda = \dfrac{6}{k}\\ \bullet k = 1 \Rightarrow \lambda = 6 \Rightarrow \dfrac{{AB}}{\lambda } = 1,666 \Rightarrow 4CT\\ \bullet k = 2 \Rightarrow \lambda = 3 \Rightarrow \dfrac{{AB}}{3} = 3,333 \Rightarrow 6CT\end{array}$
Hình vẽ

Click để xem thêm...

Bài này em nghĩ chỗ tìm vị trí của $M_1$ phải cẩn thận bởi vì chưa chắc điểm $M_1$ thỏa mãn $S_2M_1-S_1M_1=k \lambda$, đường hypebol có thể vượt ra ngoài nửa đường tròn. Chúng ta phải thử !

Kate Spencer đã viết:

Thế đáp án là bao nhiêu vậy cậu?

Click để xem thêm...

Bài này chỉ một trong hai đáp án là 4 và 6 điểm cực tiểu, như vậy đề có lẽ đã cho dư một đáp án.

datanhlg đã viết:

Bài này chỉ một trong hai đáp án là 4 và 6 điểm cực tiểu, như vậy đề có lẽ đã cho dư một đáp án.

Click để xem thêm...

Anh thử kiểm tra lại xem, chỗ $M_1$ chưa ổn lắm. Có thể một cái nào đó không thỏa mãn!

datanhlg đã viết:

Bài này chỉ một trong hai đáp án là 4 và 6 điểm cực tiểu, như vậy đề có lẽ đã cho dư một đáp án.

Click để xem thêm...

$4$ và $6$ là đường cực tiểu. Mỗi đường đó cắt đường tròn tại $2$ điểm. Vậy ta có $8$ điểm.

hoankuty đã viết:

$4$ và $6$ là đường cực tiểu. Mỗi đường đó cắt đường tròn tại $2$ điểm. Vậy ta có $8$ điểm.

Click để xem thêm...

Bất cẩn quá, lại không tính đến trường hợp này. 4 và 6 chỉ tính những cực tiểu chạy trên mặt nước.