Google
Câu hỏi: Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, $SA$ vuông góc với mặt phẳng đáy và $SA=2a$. Biết góc giữa đường thẳng $SD$ và mặt phẳng $\left( SAC \right)$ bằng ${{30}^{0}}$. Thể tích khối chóp đã cho bằng:
A. $\dfrac{8{{a}^{3}}}{3}.$
B. $\dfrac{4{{a}^{3}}}{3}.$
C. $8{{a}^{3}}.$
D. $4{{a}^{3}}.$
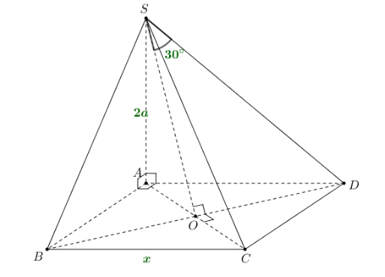Gọi $O$ là tâm của mặt đáy $ABCD.$
Dễ dàng chứng minh được: Góc giữa SD và $\left( SAC \right)$ là góc $\widehat{OSD}$. Suy ra $\widehat{OSD}={{30}^{0}}$.
Đặt $BC=x\left( x>0 \right).$ Ta tính được: $OA=OD=\dfrac{x\sqrt{2}}{2}$.
Xét $\Delta SAO$ vuông tại A: $SO=\sqrt{S{{A}^{2}}+A{{O}^{2}}}=\sqrt{4{{a}^{2}}+\dfrac{{{x}^{2}}}{2}}$.
Xét $\Delta SOD$ vuông tại O: $\tan \widehat{OSD}=\dfrac{OD}{SO}=\dfrac{x\sqrt{2}}{2}:\sqrt{4{{a}^{2}}+\dfrac{{{x}^{2}}}{2}}=\dfrac{1}{\sqrt{3}}\Leftrightarrow \dfrac{x\sqrt{2}}{2}=\dfrac{1}{\sqrt{3}}\sqrt{4{{a}^{2}}+\dfrac{{{x}^{2}}}{2}}$
$\Leftrightarrow \dfrac{{{x}^{2}}}{2}=\dfrac{1}{3}\left( 4{{a}^{2}}+\dfrac{{{x}^{2}}}{2} \right)\Leftrightarrow x=2a$. Diện tích mặt đáy ABCD là: ${{S}_{ABCD}}=A{{B}^{2}}=4{{a}^{2}}$
Vậy thể tích khối chóp $SABCD$ là: ${{V}_{S.ABCD}}=\dfrac{1}{3}.SA.{{S}_{ABCD}}=\dfrac{1}{3}.2a.4{{a}^{2}}=\dfrac{8{{a}^{3}}}{3}.$
A. $\dfrac{8{{a}^{3}}}{3}.$
B. $\dfrac{4{{a}^{3}}}{3}.$
C. $8{{a}^{3}}.$
D. $4{{a}^{3}}.$
Dễ dàng chứng minh được: Góc giữa SD và $\left( SAC \right)$ là góc $\widehat{OSD}$. Suy ra $\widehat{OSD}={{30}^{0}}$.
Đặt $BC=x\left( x>0 \right).$ Ta tính được: $OA=OD=\dfrac{x\sqrt{2}}{2}$.
Xét $\Delta SAO$ vuông tại A: $SO=\sqrt{S{{A}^{2}}+A{{O}^{2}}}=\sqrt{4{{a}^{2}}+\dfrac{{{x}^{2}}}{2}}$.
Xét $\Delta SOD$ vuông tại O: $\tan \widehat{OSD}=\dfrac{OD}{SO}=\dfrac{x\sqrt{2}}{2}:\sqrt{4{{a}^{2}}+\dfrac{{{x}^{2}}}{2}}=\dfrac{1}{\sqrt{3}}\Leftrightarrow \dfrac{x\sqrt{2}}{2}=\dfrac{1}{\sqrt{3}}\sqrt{4{{a}^{2}}+\dfrac{{{x}^{2}}}{2}}$
$\Leftrightarrow \dfrac{{{x}^{2}}}{2}=\dfrac{1}{3}\left( 4{{a}^{2}}+\dfrac{{{x}^{2}}}{2} \right)\Leftrightarrow x=2a$. Diện tích mặt đáy ABCD là: ${{S}_{ABCD}}=A{{B}^{2}}=4{{a}^{2}}$
Vậy thể tích khối chóp $SABCD$ là: ${{V}_{S.ABCD}}=\dfrac{1}{3}.SA.{{S}_{ABCD}}=\dfrac{1}{3}.2a.4{{a}^{2}}=\dfrac{8{{a}^{3}}}{3}.$
Đáp án A.