Hải Quân
Active Member
Bài toán
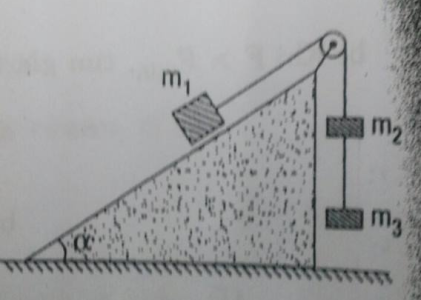
Cho hệ như hình vẽ: $m_1=1,2kg, \alpha =30^0.$ Bỏ qua kích thước của các vật, khối lượng ròng rọc và dây, ma sát. Dây nối $m_2$ và $m_3$ dài $2m.$ Khi hệ bắt đầu chuyển động,$m_3$ cách mặt đất $2m.$ Cho $g=10 \ \left(\text{m}/\text{s}^2\right).$ Biết $m_2=0,6kg, m_3=0,2kg.$
a/ Tìm gia tốc chuyển động, lực căng của các dây và thời gian chuyển động của $m_3.$
b/ Tính thời gian từ lúc $m_3$ chạm đất đến khi $m_2$ chạm đất và lực căng dây trong giai đoạn này.
C/ Bao lâu kể từ lúc $m_2$ chạm đất,$m_2$ bắt đầu đi lên?
Cho hệ như hình vẽ: $m_1=1,2kg, \alpha =30^0.$ Bỏ qua kích thước của các vật, khối lượng ròng rọc và dây, ma sát. Dây nối $m_2$ và $m_3$ dài $2m.$ Khi hệ bắt đầu chuyển động,$m_3$ cách mặt đất $2m.$ Cho $g=10 \ \left(\text{m}/\text{s}^2\right).$ Biết $m_2=0,6kg, m_3=0,2kg.$
a/ Tìm gia tốc chuyển động, lực căng của các dây và thời gian chuyển động của $m_3.$
b/ Tính thời gian từ lúc $m_3$ chạm đất đến khi $m_2$ chạm đất và lực căng dây trong giai đoạn này.
C/ Bao lâu kể từ lúc $m_2$ chạm đất,$m_2$ bắt đầu đi lên?