Bài toán
Đặt một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu một đoạn mạch như hình vẽ.
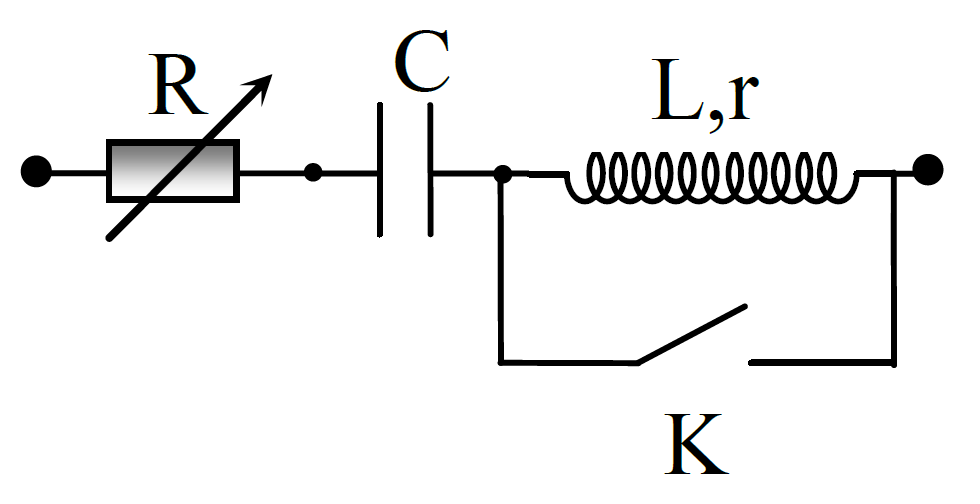
Khi K đóng, điều chỉnh giá trị biến trở đến giá trị $R_1$ hoặc $R_2$ thì công suất tỏa nhiệt trên mạch đều bằng P. Độ lệch pha giữa điện áp tức thời hai đầu mạch và dòng điện trong mạch khi $R_1$ là $\varphi _1$, khi $R=R_2$ là $\varphi _2$, trong đó $\left| \varphi _1-\varphi _2 \right|=\pi /6$. Khi K mở, điều chỉnh giá trị R từ 0 đến rất lớn thì công suất tỏa nhiệt trên biến trở R cực đại bằng 2P/3, công suất trên cả mạch cực đại bằng $2P/\sqrt{3}$. Hệ số công suất của cuộn dây là
A. $\sqrt{3}/2.$
B. 1/2.
C. $2\sqrt{3}/\sqrt{13}.$
D. $1/\sqrt{13}.$
Đặt một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu một đoạn mạch như hình vẽ.
Khi K đóng, điều chỉnh giá trị biến trở đến giá trị $R_1$ hoặc $R_2$ thì công suất tỏa nhiệt trên mạch đều bằng P. Độ lệch pha giữa điện áp tức thời hai đầu mạch và dòng điện trong mạch khi $R_1$ là $\varphi _1$, khi $R=R_2$ là $\varphi _2$, trong đó $\left| \varphi _1-\varphi _2 \right|=\pi /6$. Khi K mở, điều chỉnh giá trị R từ 0 đến rất lớn thì công suất tỏa nhiệt trên biến trở R cực đại bằng 2P/3, công suất trên cả mạch cực đại bằng $2P/\sqrt{3}$. Hệ số công suất của cuộn dây là
A. $\sqrt{3}/2.$
B. 1/2.
C. $2\sqrt{3}/\sqrt{13}.$
D. $1/\sqrt{13}.$