Nhận thấy gần đây 1 số thành viên copy đề bài với công thức dạng ảnh kiểu như sau :
Cho x,y,z là các số thực không âm thay đổi thỏa mãn:
 .
.
Tìm min:
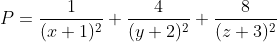
Ta có:
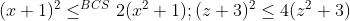
Suy ra có:
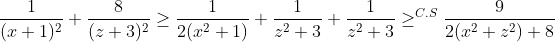
Theo bài:
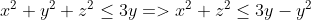
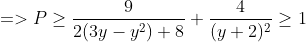
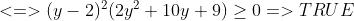
Vậy
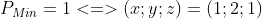
Mình đã viết 1 ứng dụng nhỏ, để tự động chuyển đổi dạng ảnh về dạng mã $\LaTeX$ của diễn đàn.
Kết quả trả về sau ghi bạn gửi nội dung trên lên diễn đàn : \left(Đã được đổi hết từ ảnh thành mã latex\right)
Cho x, y, z là các số thực không âm thay đổi thỏa mãn: $\ x^2+y^2+z^2 \le 3y$.
Tìm min: $\ P=\dfrac{1}{\left(x+1\right)^2}+\dfrac{4}{\left(y+2\right)^2}+\dfrac{8}{\left(z+3\right)^2}$
Ta có:
$\ \left(x+1\right)^2\le^{BCS} 2\left(x^2+1\right);\left(z+3\right)^2\le 4\left(z^2+3\right)$
Suy ra có:
$\ \dfrac{1}{\left(x+1\right)^2}+\dfrac{8}{\left(z+3\right)^2}\ge \dfrac{1}{2\left(x^2+1\right)}+\dfrac{1}{z^2+3}+\dfrac{1}{z^2+3}\ge^{C. S} \dfrac{9}{2\left(x^2+z^2\right)+8}$
Theo bài: $\ x^2+y^2+z^2\le 3y\Rightarrow x^2+z^2\le 3y-y^2$
$\ \Rightarrow P\ge\dfrac{9}{2\left(3y-y^2\right)+8}+\dfrac{4}{\left(y+2\right)^2}\ge 1$
$\ \Leftrightarrow \left(y-2\right)^2\left(2y^2+10y+9\right)\ge 0 \Rightarrow TRUE$
Vậy $\ P_{Min}=1\Leftrightarrow \left(x;y;z\right)=\left(1;2;1\right)$
Thân,
Lil.Tee
Cho x,y,z là các số thực không âm thay đổi thỏa mãn:
Tìm min:
Ta có:
Suy ra có:
Theo bài:
Vậy
Mình đã viết 1 ứng dụng nhỏ, để tự động chuyển đổi dạng ảnh về dạng mã $\LaTeX$ của diễn đàn.
Kết quả trả về sau ghi bạn gửi nội dung trên lên diễn đàn : \left(Đã được đổi hết từ ảnh thành mã latex\right)
Cho x, y, z là các số thực không âm thay đổi thỏa mãn: $\ x^2+y^2+z^2 \le 3y$.
Tìm min: $\ P=\dfrac{1}{\left(x+1\right)^2}+\dfrac{4}{\left(y+2\right)^2}+\dfrac{8}{\left(z+3\right)^2}$
Ta có:
$\ \left(x+1\right)^2\le^{BCS} 2\left(x^2+1\right);\left(z+3\right)^2\le 4\left(z^2+3\right)$
Suy ra có:
$\ \dfrac{1}{\left(x+1\right)^2}+\dfrac{8}{\left(z+3\right)^2}\ge \dfrac{1}{2\left(x^2+1\right)}+\dfrac{1}{z^2+3}+\dfrac{1}{z^2+3}\ge^{C. S} \dfrac{9}{2\left(x^2+z^2\right)+8}$
Theo bài: $\ x^2+y^2+z^2\le 3y\Rightarrow x^2+z^2\le 3y-y^2$
$\ \Rightarrow P\ge\dfrac{9}{2\left(3y-y^2\right)+8}+\dfrac{4}{\left(y+2\right)^2}\ge 1$
$\ \Leftrightarrow \left(y-2\right)^2\left(2y^2+10y+9\right)\ge 0 \Rightarrow TRUE$
Vậy $\ P_{Min}=1\Leftrightarrow \left(x;y;z\right)=\left(1;2;1\right)$
Thân,
Lil.Tee