Google
Câu hỏi: Cho hình trụ có hai đáy là hai hình tròn $\left( O;R \right)$ và $\left( {O}';R \right)$. $AB$ là một dây cung của đường tròn $\left( O;R \right)$ sao cho tam giác ${O}'AB$ là tam giác đều và mặt phẳng $\left( {O}'AB \right)$ tạo với mặt phẳng chứa đường tròn $\left( O;R \right)$ một góc $60{}^\circ $. Tính theo $R$ khoảng cách từ $O$ đến mặt phẳng $\left( {O}'AB \right)$.
A. $\dfrac{3R\sqrt{7}}{7}$.
B. $\dfrac{R\sqrt{7}}{7}$.
C. $\dfrac{R\sqrt{7}}{14}$.
D. $\dfrac{3R\sqrt{7}}{14}$.
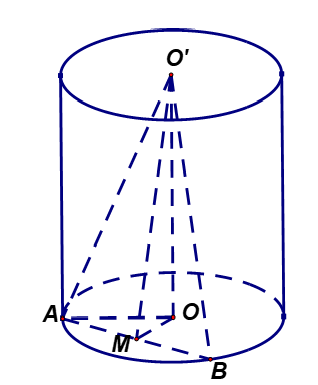Đặt độ dài cạnh $AB=x$ $\left( x>0 \right)$ và $M$ là trung điểm $AB$.
Vì tam giác ${O}'AB$ đều nên ${O}'A={O}'B=AB=x$ $\Rightarrow {O}'M=\dfrac{x\sqrt{3}}{2}$.
Vì mặt phẳng $\left( {O}'AB \right)$ tạo với mặt phẳng chứa đường tròn $\left( O;R \right)$ góc $60{}^\circ $ nên $\widehat{{O}'MO}=60{}^\circ $.
Xét tam giác ${O}'OM$ vuông tại $O$ ta có: $\cos \widehat{{O}'MO}=\dfrac{OM}{{O}'M}$. Suy ra $\cos 60{}^\circ =\dfrac{OM}{\dfrac{x\sqrt{3}}{2}}\Leftrightarrow OM=\dfrac{x\sqrt{3}}{4}$
Xét tam giác $OAM$ vuông ở $M$ có: $O{{A}^{2}}=O{{M}^{2}}+A{{M}^{2}}$ nên
${{R}^{2}}={{\left( \dfrac{x\sqrt{3}}{4} \right)}^{2}}+{{\left( \dfrac{x}{2} \right)}^{2}}\Leftrightarrow {{R}^{2}}=\dfrac{7}{16}{{x}^{2}}\Rightarrow x=\dfrac{4\sqrt{7}}{7}R$
Do đó: $OM=\dfrac{\sqrt{21}}{7}R$
Vậy khoảng cách từ $O$ đến mặt phẳng $\left( {O}'AB \right)$ là: $d\left( O;\left( O'AB \right) \right)=OM.\sin {{60}^{0}}=\dfrac{R\sqrt{21}}{7}.\dfrac{\sqrt{3}}{2}=\dfrac{3R\sqrt{7}}{14}$
A. $\dfrac{3R\sqrt{7}}{7}$.
B. $\dfrac{R\sqrt{7}}{7}$.
C. $\dfrac{R\sqrt{7}}{14}$.
D. $\dfrac{3R\sqrt{7}}{14}$.
Vì tam giác ${O}'AB$ đều nên ${O}'A={O}'B=AB=x$ $\Rightarrow {O}'M=\dfrac{x\sqrt{3}}{2}$.
Vì mặt phẳng $\left( {O}'AB \right)$ tạo với mặt phẳng chứa đường tròn $\left( O;R \right)$ góc $60{}^\circ $ nên $\widehat{{O}'MO}=60{}^\circ $.
Xét tam giác ${O}'OM$ vuông tại $O$ ta có: $\cos \widehat{{O}'MO}=\dfrac{OM}{{O}'M}$. Suy ra $\cos 60{}^\circ =\dfrac{OM}{\dfrac{x\sqrt{3}}{2}}\Leftrightarrow OM=\dfrac{x\sqrt{3}}{4}$
Xét tam giác $OAM$ vuông ở $M$ có: $O{{A}^{2}}=O{{M}^{2}}+A{{M}^{2}}$ nên
${{R}^{2}}={{\left( \dfrac{x\sqrt{3}}{4} \right)}^{2}}+{{\left( \dfrac{x}{2} \right)}^{2}}\Leftrightarrow {{R}^{2}}=\dfrac{7}{16}{{x}^{2}}\Rightarrow x=\dfrac{4\sqrt{7}}{7}R$
Do đó: $OM=\dfrac{\sqrt{21}}{7}R$
Vậy khoảng cách từ $O$ đến mặt phẳng $\left( {O}'AB \right)$ là: $d\left( O;\left( O'AB \right) \right)=OM.\sin {{60}^{0}}=\dfrac{R\sqrt{21}}{7}.\dfrac{\sqrt{3}}{2}=\dfrac{3R\sqrt{7}}{14}$
Đáp án D.