Google
Câu hỏi: Cho hình trụ tròn xoay có hai đáy là hai hình tròn $(O ; R)$ và $\left(O^{\prime} ; R\right)$. Tồn tại dây cung $A B$ thuộc đường tròn $(O)$ sao cho $\triangle O^{\prime} A B$ là tam giác đều và mặt phẳng $\left(O^{\prime} A B\right)$ hợp với mặt phẳng chứa đường tròn $(O)$ một góc $60^{\circ}$. Khi đó, diện tích xung quanh $S_{x q}$ của hình trụ và thể tích $V$ của khối trụ tương ứng là
A. $S_{x q}=\dfrac{4 \pi R^2}{7} ; V=\dfrac{2 \pi R^3 \sqrt{7}}{7}$.
B. $S_{x q}=\dfrac{6 \pi R^2 \sqrt{7}}{7} ; V=\dfrac{3 \pi R^3 \sqrt{7}}{7}$.
C. $S_{x q}=\dfrac{3 \pi R^2}{\sqrt{7}} ; V=\dfrac{2 \pi R^3 \sqrt{7}}{7}$.
D. $S_{x q}=\dfrac{3 \pi R^2 \sqrt{7}}{7} ; V=\dfrac{\pi R^3 \sqrt{7}}{7}$.
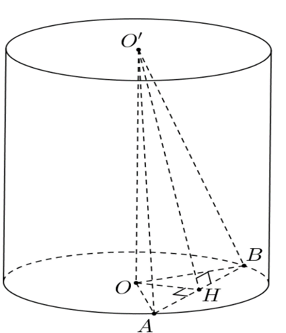Gọi $H$ là trung điểm của $A B \Rightarrow O H \perp A B(1)$.
Lại có: $O O^{\prime} \perp(O A B) \Rightarrow O O^{\prime} \perp A B(2)$.
Từ (1) và (2) suy ra $A B \perp\left(O^{\prime} O H\right) \Rightarrow A B \perp O^{\prime} H \Rightarrow \widehat{O^{\prime} H O}=60^{\circ}$
Đặt $O H=x$. Khi đó: $0<x<R$ và $O O^{\prime}=x \tan 60^{\circ}=x \sqrt{3}$.
Xét $\triangle O A H$, ta có: $A H^2=R^2-x^2$.
Vì $\triangle O^{\prime} A B$ đều nên: $O^{\prime} A=A B=2 A H=2 \sqrt{R^2-x^2}(3)$.
Mặt khác, $\triangle A O O^{\prime}$ vuông tại $O$ nên $A O^{\prime 2}=O O^{\prime 2}+R^2=3 x^2+R^2(4)$.
Từ (3), (4) ta có: $4\left(R^2-x^2\right)=3 x^2+R^2 \Leftrightarrow x^2=\dfrac{3 R^2}{7} \Leftrightarrow x=\dfrac{R \sqrt{21}}{7} \Rightarrow h=O O^{\prime}=x \sqrt{3}=\dfrac{3 R \sqrt{7}}{7}$.
Vậy: $S_{x q}=2 \pi R h=\dfrac{6 \pi R^2 \sqrt{7}}{7} ; V=\pi R^2 h=\dfrac{3 \pi R^3 \sqrt{7}}{7}$
A. $S_{x q}=\dfrac{4 \pi R^2}{7} ; V=\dfrac{2 \pi R^3 \sqrt{7}}{7}$.
B. $S_{x q}=\dfrac{6 \pi R^2 \sqrt{7}}{7} ; V=\dfrac{3 \pi R^3 \sqrt{7}}{7}$.
C. $S_{x q}=\dfrac{3 \pi R^2}{\sqrt{7}} ; V=\dfrac{2 \pi R^3 \sqrt{7}}{7}$.
D. $S_{x q}=\dfrac{3 \pi R^2 \sqrt{7}}{7} ; V=\dfrac{\pi R^3 \sqrt{7}}{7}$.
Lại có: $O O^{\prime} \perp(O A B) \Rightarrow O O^{\prime} \perp A B(2)$.
Từ (1) và (2) suy ra $A B \perp\left(O^{\prime} O H\right) \Rightarrow A B \perp O^{\prime} H \Rightarrow \widehat{O^{\prime} H O}=60^{\circ}$
Đặt $O H=x$. Khi đó: $0<x<R$ và $O O^{\prime}=x \tan 60^{\circ}=x \sqrt{3}$.
Xét $\triangle O A H$, ta có: $A H^2=R^2-x^2$.
Vì $\triangle O^{\prime} A B$ đều nên: $O^{\prime} A=A B=2 A H=2 \sqrt{R^2-x^2}(3)$.
Mặt khác, $\triangle A O O^{\prime}$ vuông tại $O$ nên $A O^{\prime 2}=O O^{\prime 2}+R^2=3 x^2+R^2(4)$.
Từ (3), (4) ta có: $4\left(R^2-x^2\right)=3 x^2+R^2 \Leftrightarrow x^2=\dfrac{3 R^2}{7} \Leftrightarrow x=\dfrac{R \sqrt{21}}{7} \Rightarrow h=O O^{\prime}=x \sqrt{3}=\dfrac{3 R \sqrt{7}}{7}$.
Vậy: $S_{x q}=2 \pi R h=\dfrac{6 \pi R^2 \sqrt{7}}{7} ; V=\pi R^2 h=\dfrac{3 \pi R^3 \sqrt{7}}{7}$
Đáp án B.