Cho $x, y$ là các số thực thỏa mãn $x>y>1.$ Biểu thức $A=\log...

Ta có: $A=\log _{\dfrac{x}{y}}^{2}{{x}^{3}}+\dfrac{8}{3}{{\log }_{y}}\left( \dfrac{x}{y} \right)=\dfrac{9}{{{\log }_{x}}^{2}\dfrac{x}{y}}+\dfrac{8}{3}.\left[ {{\log }_{y}}x-1 \right]=\dfrac{9}{{{\left( 1-{{\log }_{x}}y \right)}^{2}}}+\dfrac{8}{3.{{\log }_{x}}y}-\dfrac{8}{3}$
Đặt ${{\log }_{x}}y=t$ ( ${{\log }_{x}}y>{{\log }_{x}}1=0\Rightarrow t>0$ và $x>y\Rightarrow {{\log }_{x}}x>{{\log }_{x}}y\Rightarrow 1>t$ )
Suy ra $0<t<1$. Khi đó A trở thành: $A=\dfrac{9}{{{\left( 1-t \right)}^{2}}}+\dfrac{8}{3t}-\dfrac{8}{3}=f(t)$
Xét hàm số $f(t)=\dfrac{9}{{{\left( t-1 \right)}^{2}}}+\dfrac{8}{3t}-\dfrac{8}{3}$ có $f'(t)=-\dfrac{2.9}{{{\left( t-1 \right)}^{3}}}-\dfrac{8}{3{{t}^{2}}}=0\Leftrightarrow \left[ \begin{aligned}
& t=\dfrac{1}{4} (tm) \\
& t=-2 (loai) \\
\end{aligned} \right.$
Ta có bảng biến thiên
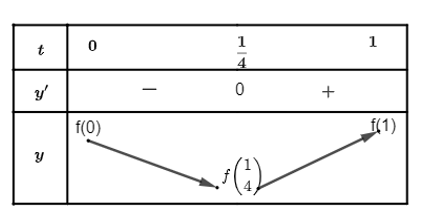Vậy A đạt giá trị nhỏ nhất khi $t=\dfrac{1}{4}\Rightarrow {{\log }_{x}}y=\dfrac{1}{4}\Rightarrow x={{y}^{4}}$.