Câu hỏi: Chứng minh rằng với mọi góc \(α (0^0≤ α ≤ 180^0)\) ta đều có \(\sin ^2\alpha + {\cos ^2}\alpha = 1.\)
Lời giải chi tiết
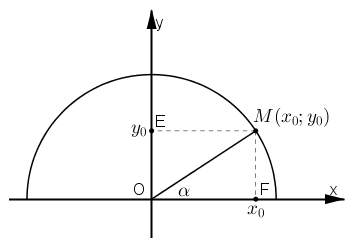
Vẽ nửa đường tròn lượng giác (O; 1).
Với mọi α (0º ≤ α ≤ 180º) ta đều có điểm M(x0; y0) thuộc nửa đường tròn sao cho \(\widehat {xOM} = \alpha \)
Khi đó ta có: sin α = y0 ; cos α = x0.
Mà M thuộc đường tròn lượng giác nên OM=1.
Ta có:
\(\begin{array}{l}
{\sin ^2}\alpha + {\cos ^2}\alpha = y_0^2 + x_0^2\\
= O{E^2} + O{F^2} = M{F^2} + O{F^2}\\
= O{M^2} = {1^2} = 1\\
\Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1
\end{array}\)
Cách khác:
TH1: \(\alpha = {0^0}\) thì \({\sin ^2}\alpha + {\cos ^2}\alpha = {\sin ^2}0^0 + {\cos ^2}0^0 \) \(=0^2+1^2= 1\)
TH2: \(\alpha = {180^0}\) thì \({\sin ^2}\alpha + {\cos ^2}\alpha = {\sin ^2}180^0 + {\cos ^2}180 ^0\) \(=0^2+(-1)^2= 1\)
TH3: \(0^0 < \alpha < {90^0}\).
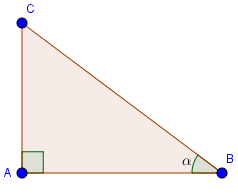
Xét tam giác \(ABC\) vuông tại \(A\), đặt \(\widehat B = \alpha \) có:
\(\sin \alpha = \sin B = \dfrac{{AC}}{{BC}},\) \(\cos \alpha = \cos B = \dfrac{{AB}}{{BC}}\)
\(\Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha \) \(= {\left( {\dfrac{{AC}}{{BC}}} \right)^2} + {\left({\dfrac{{AB}}{{BC}}} \right)^2}\) \(= \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \dfrac{{B{C^2}}}{{B{C^2}}} = 1\)
TH4: \({90^0} < \alpha < {180^0}\).
\(\Rightarrow {0^0} < {180^0} - \alpha < {90^0} \)
\(\Rightarrow {\sin ^2}\left( {{{180}^0} - \alpha } \right) + {\cos ^2}\left({{{180}^0} - \alpha } \right)=1\) (áp dụng TH3)
\( \Rightarrow {\sin ^2}\alpha + {\left( { - \cos \alpha } \right)^2} =1\) (vì \(\sin \left( {{{180}^0} - \alpha } \right) = \sin \alpha ,\) \(\cos \left( {{{180}^0} - \alpha } \right) = - \cos \alpha \))
\(\Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Vậy ta có đpcm.
Vẽ nửa đường tròn lượng giác (O; 1).
Với mọi α (0º ≤ α ≤ 180º) ta đều có điểm M(x0; y0) thuộc nửa đường tròn sao cho \(\widehat {xOM} = \alpha \)
Khi đó ta có: sin α = y0 ; cos α = x0.
Mà M thuộc đường tròn lượng giác nên OM=1.
Ta có:
\(\begin{array}{l}
{\sin ^2}\alpha + {\cos ^2}\alpha = y_0^2 + x_0^2\\
= O{E^2} + O{F^2} = M{F^2} + O{F^2}\\
= O{M^2} = {1^2} = 1\\
\Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1
\end{array}\)
Cách khác:
TH1: \(\alpha = {0^0}\) thì \({\sin ^2}\alpha + {\cos ^2}\alpha = {\sin ^2}0^0 + {\cos ^2}0^0 \) \(=0^2+1^2= 1\)
TH2: \(\alpha = {180^0}\) thì \({\sin ^2}\alpha + {\cos ^2}\alpha = {\sin ^2}180^0 + {\cos ^2}180 ^0\) \(=0^2+(-1)^2= 1\)
TH3: \(0^0 < \alpha < {90^0}\).
Xét tam giác \(ABC\) vuông tại \(A\), đặt \(\widehat B = \alpha \) có:
\(\sin \alpha = \sin B = \dfrac{{AC}}{{BC}},\) \(\cos \alpha = \cos B = \dfrac{{AB}}{{BC}}\)
\(\Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha \) \(= {\left( {\dfrac{{AC}}{{BC}}} \right)^2} + {\left({\dfrac{{AB}}{{BC}}} \right)^2}\) \(= \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \dfrac{{B{C^2}}}{{B{C^2}}} = 1\)
TH4: \({90^0} < \alpha < {180^0}\).
\(\Rightarrow {0^0} < {180^0} - \alpha < {90^0} \)
\(\Rightarrow {\sin ^2}\left( {{{180}^0} - \alpha } \right) + {\cos ^2}\left({{{180}^0} - \alpha } \right)=1\) (áp dụng TH3)
\( \Rightarrow {\sin ^2}\alpha + {\left( { - \cos \alpha } \right)^2} =1\) (vì \(\sin \left( {{{180}^0} - \alpha } \right) = \sin \alpha ,\) \(\cos \left( {{{180}^0} - \alpha } \right) = - \cos \alpha \))
\(\Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Vậy ta có đpcm.