Google
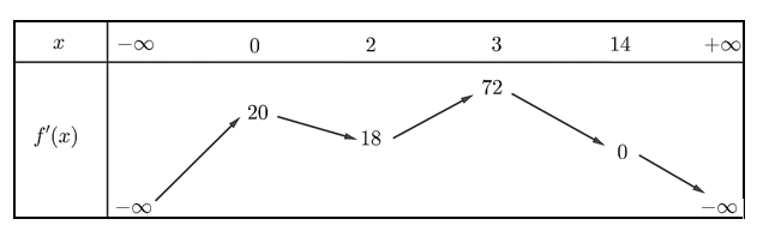
Câu hỏi: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên của ${f}'\left( x \right)$ như sau:
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số $m$ trên đoạn $\left[ -2022;2023 \right]$ để hàm số $g\left( x \right)=f\left( \dfrac{{{x}^{3}}}{9} \right)-\dfrac{m{{\left( {{x}^{2}}+9 \right)}^{2}}}{18}$ nghịch biến trên khoảng $\left( 0;5 \right)$ ?
A. $2005.$
B. $2006.$
C. $2004.$
D. $2007.$
A. $2005.$
B. $2006.$
C. $2004.$
D. $2007.$
Đặt $t=\dfrac{{{x}^{3}}}{9}\Rightarrow {t}'=\dfrac{{{x}^{2}}}{3}\ge {{0}^{{}}}\forall x\in \left( 0;5 \right)\Rightarrow t\in \left( 0;\dfrac{{{5}^{3}}}{9} \right)$. Ta có $t=\dfrac{{{x}^{3}}}{9}\Leftrightarrow x=\sqrt[3]{9t}\Leftrightarrow {{x}^{2}}=3\sqrt[3]{3}{{t}^{\dfrac{2}{3}}}$.
Khi đó ta cần tìm $m$ để hàm số $h\left( t \right)=f\left( t \right)-\dfrac{m{{\left( \sqrt[3]{3}{{t}^{\dfrac{2}{3}}}+3 \right)}^{2}}}{2}$ nghịch biến trên $\left( 0;\dfrac{{{5}^{3}}}{9} \right)$.
Ta có ${h}'\left( t \right)={f}'\left( t \right)-\dfrac{2}{3}\sqrt[3]{3}.m\left( \sqrt[3]{3}{{t}^{\dfrac{2}{3}}}+3 \right){{t}^{\dfrac{-1}{3}}}={f}'\left( t \right)-\dfrac{2}{3}\sqrt[3]{3}.m\left( \sqrt[3]{3}{{t}^{\dfrac{1}{3}}}+3{{t}^{\dfrac{-1}{3}}} \right)$.
Để $h\left( t \right)$ nghịch biến trên $\left( 0;\dfrac{{{5}^{3}}}{9} \right)$ $\Leftrightarrow {h}'\left( t \right)={f}'\left( t \right)-\dfrac{2}{3}\sqrt[3]{3}.m\left( \sqrt[3]{3}{{t}^{\dfrac{1}{3}}}+3{{t}^{\dfrac{-1}{3}}} \right)\le {{0}^{{}}}\forall t\in \left( 0;\dfrac{{{5}^{3}}}{9} \right)$
$\Leftrightarrow m\ge \dfrac{{f}'\left( t \right)}{u\left( t \right)}\forall t\in \left( 0;\dfrac{{{5}^{3}}}{9} \right)$ với $u\left( t \right)=\dfrac{2}{3}\sqrt[3]{3}\left( \sqrt[3]{3}{{t}^{\dfrac{1}{3}}}+3{{t}^{\dfrac{-1}{3}}} \right)$
Ta có ${u}'\left( t \right)=\dfrac{2}{9}\sqrt[3]{3}\left( \sqrt[3]{3}{{t}^{\dfrac{-2}{3}}}-3{{t}^{\dfrac{-4}{3}}} \right)$. Ta có ${u}'\left( t \right)=0\Leftrightarrow \sqrt[3]{3}{{t}^{\dfrac{-2}{3}}}-3{{t}^{\dfrac{-4}{3}}}=0\Leftrightarrow t=3$.
Bảng biến thiên:
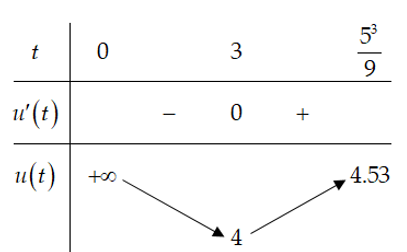Từ bảng biến thiên ta thấy được $u\left( t \right)\ge u{{\left( 3 \right)}^{{}}}\forall t\in \left( 0;\dfrac{{{5}^{3}}}{9} \right)$, mà ${f}'\left( t \right)\le {f}'{{\left( 3 \right)}^{{}}}\forall t\in \left( 0;\dfrac{{{5}^{3}}}{9} \right)$
Khi đó $m\ge \dfrac{{f}'\left( t \right)}{u\left( t \right)}\forall t\in \left( 0;\dfrac{{{5}^{3}}}{9} \right)\Leftrightarrow m\ge \dfrac{{f}'\left( 3 \right)}{u\left( 3 \right)}=18$.
Khi đó ta cần tìm $m$ để hàm số $h\left( t \right)=f\left( t \right)-\dfrac{m{{\left( \sqrt[3]{3}{{t}^{\dfrac{2}{3}}}+3 \right)}^{2}}}{2}$ nghịch biến trên $\left( 0;\dfrac{{{5}^{3}}}{9} \right)$.
Ta có ${h}'\left( t \right)={f}'\left( t \right)-\dfrac{2}{3}\sqrt[3]{3}.m\left( \sqrt[3]{3}{{t}^{\dfrac{2}{3}}}+3 \right){{t}^{\dfrac{-1}{3}}}={f}'\left( t \right)-\dfrac{2}{3}\sqrt[3]{3}.m\left( \sqrt[3]{3}{{t}^{\dfrac{1}{3}}}+3{{t}^{\dfrac{-1}{3}}} \right)$.
Để $h\left( t \right)$ nghịch biến trên $\left( 0;\dfrac{{{5}^{3}}}{9} \right)$ $\Leftrightarrow {h}'\left( t \right)={f}'\left( t \right)-\dfrac{2}{3}\sqrt[3]{3}.m\left( \sqrt[3]{3}{{t}^{\dfrac{1}{3}}}+3{{t}^{\dfrac{-1}{3}}} \right)\le {{0}^{{}}}\forall t\in \left( 0;\dfrac{{{5}^{3}}}{9} \right)$
$\Leftrightarrow m\ge \dfrac{{f}'\left( t \right)}{u\left( t \right)}\forall t\in \left( 0;\dfrac{{{5}^{3}}}{9} \right)$ với $u\left( t \right)=\dfrac{2}{3}\sqrt[3]{3}\left( \sqrt[3]{3}{{t}^{\dfrac{1}{3}}}+3{{t}^{\dfrac{-1}{3}}} \right)$
Ta có ${u}'\left( t \right)=\dfrac{2}{9}\sqrt[3]{3}\left( \sqrt[3]{3}{{t}^{\dfrac{-2}{3}}}-3{{t}^{\dfrac{-4}{3}}} \right)$. Ta có ${u}'\left( t \right)=0\Leftrightarrow \sqrt[3]{3}{{t}^{\dfrac{-2}{3}}}-3{{t}^{\dfrac{-4}{3}}}=0\Leftrightarrow t=3$.
Bảng biến thiên:
Khi đó $m\ge \dfrac{{f}'\left( t \right)}{u\left( t \right)}\forall t\in \left( 0;\dfrac{{{5}^{3}}}{9} \right)\Leftrightarrow m\ge \dfrac{{f}'\left( 3 \right)}{u\left( 3 \right)}=18$.
Đáp án B.