Google
Câu hỏi: Cho hình nón $(H)$ có đỉnh $S$ và đáy là hình tròn tâm $O$, bán kính $R$, chiều cao $2 R$. Một mặt phẳng đi qua đỉnh và cắt đường tròn đáy theo dây cung $A B$ có độ dài bằng bán kính đáy. Tính sin của góc tạo bởi $O A$ và mặt phẳng $(S A B)$.
A. $\dfrac{\sqrt{3}}{4}$.
B. $\dfrac{2 \sqrt{57}}{19}$.
C. $\dfrac{\sqrt{3}}{2}$.
D. $\dfrac{\sqrt{57}}{19}$.
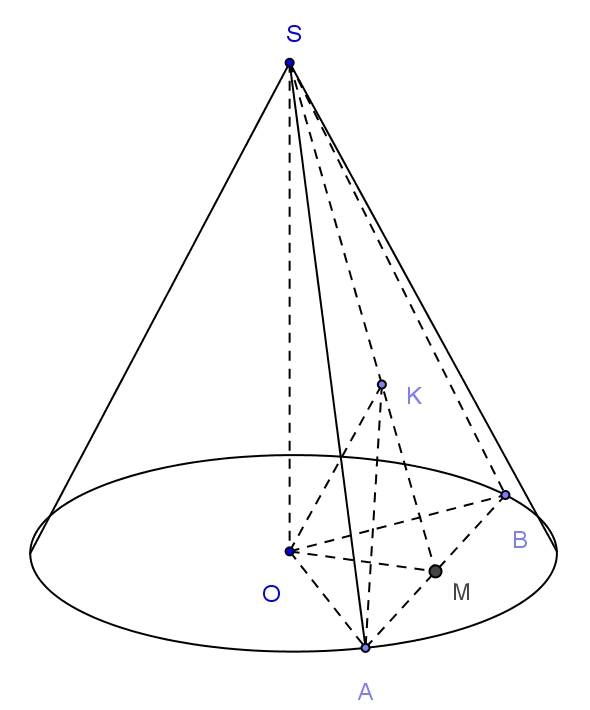+ Xác định góc tạo bời $O A$ và mặt phẳng $(S A B)$
Kè $O M \perp A B, M \in A B$ ( $M$ là trung điểm $A B)$, kè $O K \perp S M, K \in S M$. Chứng minh $O K \perp(S A B)$. Thật vậy: $O K \perp S M$ (theo cách kè), $O K \perp A B$ (Vì $A B \perp(S O M)$, do $O M \perp A B$ và $A B \perp S O$ ). Suy ra: hình chiếu vuông góc của $O A$ trên mặt phẳng $(S A B)$ là $A K$. Vậy góc tạo bời $O A$ và mặt phẳng $(S A B)$ là góc taọ bởi hai đường thẳng $O A$ và $A K$ hay góc $\overline{O A K}$ + Tính sin c ủa góc $\widehat{O A K}$
Tam giác $O A B$ đều, cạnh là $R$ nên $O M=\dfrac{R \sqrt{3}}{2}$. Xét tam giác vuông $S O M$ có
$
\dfrac{1}{O K^2}=\dfrac{1}{O A^2}+\dfrac{1}{O M^2}=\dfrac{1}{(2 R)^2}+\dfrac{1}{\left(\dfrac{R \sqrt{3}}{2}\right)^2}=\dfrac{19}{12 R^2} \Rightarrow O K=\dfrac{2 R \sqrt{57}}{19}
$
Trong tam giác vuông $O K A$ (vuông tại $K$ ), có $\sin \widehat{O A K}=\dfrac{O K}{O A}=\dfrac{2 R \sqrt{57}}{19 R}=\dfrac{2 \sqrt{57}}{19}$.
A. $\dfrac{\sqrt{3}}{4}$.
B. $\dfrac{2 \sqrt{57}}{19}$.
C. $\dfrac{\sqrt{3}}{2}$.
D. $\dfrac{\sqrt{57}}{19}$.
Kè $O M \perp A B, M \in A B$ ( $M$ là trung điểm $A B)$, kè $O K \perp S M, K \in S M$. Chứng minh $O K \perp(S A B)$. Thật vậy: $O K \perp S M$ (theo cách kè), $O K \perp A B$ (Vì $A B \perp(S O M)$, do $O M \perp A B$ và $A B \perp S O$ ). Suy ra: hình chiếu vuông góc của $O A$ trên mặt phẳng $(S A B)$ là $A K$. Vậy góc tạo bời $O A$ và mặt phẳng $(S A B)$ là góc taọ bởi hai đường thẳng $O A$ và $A K$ hay góc $\overline{O A K}$ + Tính sin c ủa góc $\widehat{O A K}$
Tam giác $O A B$ đều, cạnh là $R$ nên $O M=\dfrac{R \sqrt{3}}{2}$. Xét tam giác vuông $S O M$ có
$
\dfrac{1}{O K^2}=\dfrac{1}{O A^2}+\dfrac{1}{O M^2}=\dfrac{1}{(2 R)^2}+\dfrac{1}{\left(\dfrac{R \sqrt{3}}{2}\right)^2}=\dfrac{19}{12 R^2} \Rightarrow O K=\dfrac{2 R \sqrt{57}}{19}
$
Trong tam giác vuông $O K A$ (vuông tại $K$ ), có $\sin \widehat{O A K}=\dfrac{O K}{O A}=\dfrac{2 R \sqrt{57}}{19 R}=\dfrac{2 \sqrt{57}}{19}$.
Đáp án B.
