Google
Câu hỏi: Trong không gian $Oxyz$, cho mặt cầu $\left( S \right)$ : ${{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=27$, Gọi $\left( \alpha \right)$ là mặt phẳng đi qua hai điểm $A(0 ; 0 ;-4), B(2 ; 0 ; 0)$ và cắt $\left( S \right)$ theo giao tuyến là đường tròn $\left( C \right)$ sao cho khối nón đỉnh là tâm của $\left( S \right)$ và đáy là $\left( C \right)$ có thể tích lớn nhất. Biết phương trình của $\left( \alpha \right)$ có dạng $a x+b y-z+c=0,(a, b, c \in \mathbb{R})$. Giá trị của $a-b+c$ bằng
A. $-4$.
B. 0.
C. 8.
D. 2.
A. $-4$.
B. 0.
C. 8.
D. 2.
Mặt cầu $\left( S \right)$ có tâm $I\left( 1; -2; 3 \right)$ và bán kính $R=3\sqrt{3}$.
Điểm $A\left( 0;0;-4 \right)\in \left( \alpha \right)\Rightarrow 4+c=0\Rightarrow c=-4$.
Điểm $B\left( 2;0;0 \right)\in \left( \alpha \right)\Rightarrow 2a+c=0\Rightarrow a=-\dfrac{c}{2}=2$.
Mặt phẳng $\left( \alpha \right)$ có dạng $2x+by-z-4=0$.
Gọi $d$ là khoảng cách từ tâm $I$ đến mặt phẳng $\left( \alpha \right)$ và $r$ là bán kính của đường tròn $\left( C \right)$.
Khi đó khối nón có đỉnh $I$ và đáy là đường tròn $\left( C \right)$ có thể tích là:
$V=\dfrac{1}{3}\pi {{r}^{2}}d=\dfrac{1}{3}\pi \left( {{R}^{2}}-{{d}^{2}} \right)d=\dfrac{1}{3}\pi \left( 27-{{d}^{2}} \right)d$
Đặt $f\left( d \right)=\left( 27-{{d}^{2}} \right)d=-{{d}^{3}}+27d, \left( 0<d<3\sqrt{3} \right)$.
Suy ra ${f}'\left( d \right)=-3{{d}^{2}}+27$ và ${f}'\left( d \right)=0\Leftrightarrow -3{{d}^{2}}+27=0\Leftrightarrow d=3$ (vì $0<d<3\sqrt{3}$ ).
Bảng biến thiên:
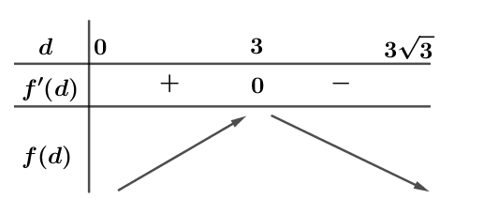Dựa vào bảng biến thiên, ta thấy $f\left( d \right)$ đạt giá trị lớn nhất khi $d=3$ hay thể tích khối nón đạt giá trị lớn nhất khi $d=3\Leftrightarrow {{d}^{2}}=9$.
Mà $d=d\left( I,\left( \alpha \right) \right)=\dfrac{\left| -5-2b \right|}{\sqrt{5+{{b}^{2}}}}$ nên $\dfrac{{{\left( -5-2b \right)}^{2}}}{5+{{b}^{2}}}=9\Leftrightarrow 5{{b}^{2}}-20b+20=0\Leftrightarrow b=2$.
Vậy $a-b+c=-4$.
Điểm $A\left( 0;0;-4 \right)\in \left( \alpha \right)\Rightarrow 4+c=0\Rightarrow c=-4$.
Điểm $B\left( 2;0;0 \right)\in \left( \alpha \right)\Rightarrow 2a+c=0\Rightarrow a=-\dfrac{c}{2}=2$.
Mặt phẳng $\left( \alpha \right)$ có dạng $2x+by-z-4=0$.
Gọi $d$ là khoảng cách từ tâm $I$ đến mặt phẳng $\left( \alpha \right)$ và $r$ là bán kính của đường tròn $\left( C \right)$.
Khi đó khối nón có đỉnh $I$ và đáy là đường tròn $\left( C \right)$ có thể tích là:
$V=\dfrac{1}{3}\pi {{r}^{2}}d=\dfrac{1}{3}\pi \left( {{R}^{2}}-{{d}^{2}} \right)d=\dfrac{1}{3}\pi \left( 27-{{d}^{2}} \right)d$
Đặt $f\left( d \right)=\left( 27-{{d}^{2}} \right)d=-{{d}^{3}}+27d, \left( 0<d<3\sqrt{3} \right)$.
Suy ra ${f}'\left( d \right)=-3{{d}^{2}}+27$ và ${f}'\left( d \right)=0\Leftrightarrow -3{{d}^{2}}+27=0\Leftrightarrow d=3$ (vì $0<d<3\sqrt{3}$ ).
Bảng biến thiên:
Mà $d=d\left( I,\left( \alpha \right) \right)=\dfrac{\left| -5-2b \right|}{\sqrt{5+{{b}^{2}}}}$ nên $\dfrac{{{\left( -5-2b \right)}^{2}}}{5+{{b}^{2}}}=9\Leftrightarrow 5{{b}^{2}}-20b+20=0\Leftrightarrow b=2$.
Vậy $a-b+c=-4$.
Đáp án A.
