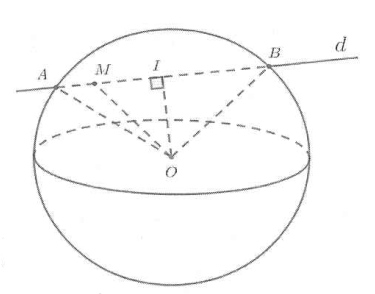
Câu hỏi: Trong không gian với hệ tọa độ Oxyz, cho ba điểm P, Q, R lần lượt di động trên ba trục tọa độ Ox, Oy, Oz (không trùng với gốc tọa độ O) sao cho $\dfrac{1}{O{{P}^{2}}}+\dfrac{1}{O{{Q}^{2}}}+\dfrac{1}{O{{R}^{2}}}=\dfrac{1}{8}.$ Biết mặt phẳng $\left( PQR \right)$ luôn tiếp xúc với mặt cầu $\left( S \right)$ cố định. Đường thẳng d thay đổi nhưng luôn đi qua $M\left( \dfrac{1}{2};\dfrac{\sqrt{3}}{2};0 \right)$ và cắt $\left( S \right)$ tại hai điểm A, B phân biệt. Diện tích lớn nhất của tam giác AOB là.
A. $\sqrt{15}.$
B. $\sqrt{5}.$
C. $\sqrt{17}.$
D. $\sqrt{7}.$
A. $\sqrt{15}.$
B. $\sqrt{5}.$
C. $\sqrt{17}.$
D. $\sqrt{7}.$
Gọi H là hình chiếu vuông góc của điểm trên O trên mặt phẳng $\left( PQR \right).$
Dễ thấy $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{P}^{2}}}+\dfrac{1}{O{{Q}^{2}}}+\dfrac{1}{O{{R}^{2}}}$ suy ra $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{8}$ hay $OH=2\sqrt{2}.$
Khi đó suy ra mặt phẳng $\left( PQR \right)$ luôn tiếp xúc với mặt cầu $\left( S \right)$ tâm O, bán kính
$z=x+yi\left( x,y\in \mathbb{R} \right);x+yi\ne 2.$
Ta có $\left( C \right)$ nên điểm $\dfrac{{{x}^{2}}}{25}+\dfrac{{{y}^{2}}}{16}=1\Rightarrow y=\pm 4\sqrt{1-\dfrac{{{x}^{2}}}{25}}$ nằm trong mặt cầu
$S=4\int\limits_{0}^{4}{\left( \sqrt{36-{{x}^{2}}}-4\sqrt{1-\dfrac{{{x}^{2}}}{25}} \right)}dx\simeq 30,03{{m}^{2}}.$
Gọi $\left\{ \begin{aligned}
& f\left( 0 \right)=c \\
& f\left( 1 \right)=a+b+c+\dfrac{1}{6} \\
& f\left( 2 \right)=4a+2b+c+\dfrac{4}{3} \\
\end{aligned} \right. $ là trung điểm của $ \Rightarrow \left\{ \begin{aligned}
& a+b=\dfrac{-1}{6} \\
& 4a+2b=\dfrac{-4}{3} \\
\end{aligned} \right., $ do tam giác $ \Leftrightarrow \left\{ \begin{aligned}
& a=-\dfrac{1}{2} \\
& b=\dfrac{1}{3} \\
\end{aligned} \right. $ cân tại O nên $ f\left( x \right)=\dfrac{1}{6}{{x}^{3}}-\dfrac{1}{2}{{x}^{2}}+\dfrac{1}{3}x+c.$
Đặt $g\left( x \right),$ vì $\left( 0;1 \right)$ nên ${g}'\left( x \right)=2x{f}'\left( {{x}^{2}}+2 \right){f}'\left[ f\left( {{x}^{2}}+2 \right) \right]\le 0$ và $\forall x\in \left( 0;1 \right).$
Ta có ${f}'\left( x \right)=\dfrac{1}{2}{{x}^{2}}-x+\dfrac{1}{3}.$
Xét hàm số $\forall x\in \left( 0;1 \right)$ với ${g}'\left( x \right)\le 0\Leftrightarrow {f}'\left[ f\left( {{x}^{2}}+2 \right) \right]\le 0.$
Có $0<x<1\Rightarrow 2<{{x}^{2}}+2<3$ với mọi ${f}'\left( x \right)>0\forall x\in \left( 2;3 \right)$ $f\left( x \right).$
Suy ra diện tích của tam giác $\left( 2;3 \right)$ lớn nhất bằng $f\left( 2 \right)<f\left( {{x}^{2}}+2 \right)<f\left( 3 \right)$ đạt được khi M là trung điểm của $1-\dfrac{\sqrt{3}}{3}\le f\left( 2 \right)<f\left( 3 \right)\le 1+\dfrac{\sqrt{3}}{3}.$
Cách 2. $\Leftrightarrow \left\{ \begin{aligned}
& f\left( 2 \right)\ge 1-\dfrac{\sqrt{3}}{3} \\
& f\left( 3 \right)\le 1+\dfrac{\sqrt{3}}{3} \\
\end{aligned} \right. $ với $ \Rightarrow 1-\dfrac{\sqrt{3}}{3}\le c\le 1+\dfrac{\sqrt{3}}{3}.$
Bước 2: Khảo sát sự biến thiên của hàm biến x để suy ra giá trị lớn nhất và giá trị nhỏ nhất.
Dễ thấy $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{P}^{2}}}+\dfrac{1}{O{{Q}^{2}}}+\dfrac{1}{O{{R}^{2}}}$ suy ra $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{8}$ hay $OH=2\sqrt{2}.$
Khi đó suy ra mặt phẳng $\left( PQR \right)$ luôn tiếp xúc với mặt cầu $\left( S \right)$ tâm O, bán kính
$z=x+yi\left( x,y\in \mathbb{R} \right);x+yi\ne 2.$
Ta có $\left( C \right)$ nên điểm $\dfrac{{{x}^{2}}}{25}+\dfrac{{{y}^{2}}}{16}=1\Rightarrow y=\pm 4\sqrt{1-\dfrac{{{x}^{2}}}{25}}$ nằm trong mặt cầu
$S=4\int\limits_{0}^{4}{\left( \sqrt{36-{{x}^{2}}}-4\sqrt{1-\dfrac{{{x}^{2}}}{25}} \right)}dx\simeq 30,03{{m}^{2}}.$
Gọi $\left\{ \begin{aligned}
& f\left( 0 \right)=c \\
& f\left( 1 \right)=a+b+c+\dfrac{1}{6} \\
& f\left( 2 \right)=4a+2b+c+\dfrac{4}{3} \\
\end{aligned} \right. $ là trung điểm của $ \Rightarrow \left\{ \begin{aligned}
& a+b=\dfrac{-1}{6} \\
& 4a+2b=\dfrac{-4}{3} \\
\end{aligned} \right., $ do tam giác $ \Leftrightarrow \left\{ \begin{aligned}
& a=-\dfrac{1}{2} \\
& b=\dfrac{1}{3} \\
\end{aligned} \right. $ cân tại O nên $ f\left( x \right)=\dfrac{1}{6}{{x}^{3}}-\dfrac{1}{2}{{x}^{2}}+\dfrac{1}{3}x+c.$
Đặt $g\left( x \right),$ vì $\left( 0;1 \right)$ nên ${g}'\left( x \right)=2x{f}'\left( {{x}^{2}}+2 \right){f}'\left[ f\left( {{x}^{2}}+2 \right) \right]\le 0$ và $\forall x\in \left( 0;1 \right).$
Ta có ${f}'\left( x \right)=\dfrac{1}{2}{{x}^{2}}-x+\dfrac{1}{3}.$
Xét hàm số $\forall x\in \left( 0;1 \right)$ với ${g}'\left( x \right)\le 0\Leftrightarrow {f}'\left[ f\left( {{x}^{2}}+2 \right) \right]\le 0.$
Có $0<x<1\Rightarrow 2<{{x}^{2}}+2<3$ với mọi ${f}'\left( x \right)>0\forall x\in \left( 2;3 \right)$ $f\left( x \right).$
Suy ra diện tích của tam giác $\left( 2;3 \right)$ lớn nhất bằng $f\left( 2 \right)<f\left( {{x}^{2}}+2 \right)<f\left( 3 \right)$ đạt được khi M là trung điểm của $1-\dfrac{\sqrt{3}}{3}\le f\left( 2 \right)<f\left( 3 \right)\le 1+\dfrac{\sqrt{3}}{3}.$
Cách 2. $\Leftrightarrow \left\{ \begin{aligned}
& f\left( 2 \right)\ge 1-\dfrac{\sqrt{3}}{3} \\
& f\left( 3 \right)\le 1+\dfrac{\sqrt{3}}{3} \\
\end{aligned} \right. $ với $ \Rightarrow 1-\dfrac{\sqrt{3}}{3}\le c\le 1+\dfrac{\sqrt{3}}{3}.$
Note 47: Phương pháp chung
Bước 1: Xác định yếu tố thay đổi của bài toán và tính toán các yếu tố đề yêu cầu theo biến số, cụ thể ở bài này là biến x.Bước 2: Khảo sát sự biến thiên của hàm biến x để suy ra giá trị lớn nhất và giá trị nhỏ nhất.
Đáp án D.