Câu hỏi: Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right)$ có phương trình là ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-4x+2y-2z-3=0$ và điểm $A\left( 5;3;-2 \right)$. Một đường thẳng $d$ thay đổi luôn đi qua $A$ và luôn cắt mặt cầu tại hai điểm phân biệt $M,N$. Tính giá trị nhỏ nhất của biểu thức $S=AM+4AN$.
A. ${{S}_{\min }}=30$.
B. ${{S}_{\min }}=20$.
C. ${{S}_{\min }}=\sqrt{34}-3$.
D. ${{S}_{\min }}=5\sqrt{34}-9$.
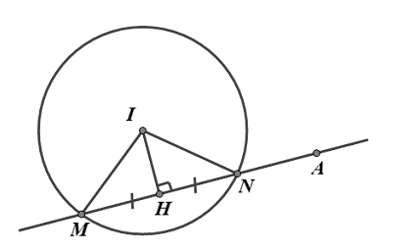 Mặt cầu $\left( S \right)$ có tâm $I\left( 2; -1; 1 \right)$, bán kính $R=\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}+{{1}^{2}}-\left( -3 \right)}=3$.
Mặt cầu $\left( S \right)$ có tâm $I\left( 2; -1; 1 \right)$, bán kính $R=\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}+{{1}^{2}}-\left( -3 \right)}=3$.
Ta có $AI=\sqrt{{{\left( 2-5 \right)}^{2}}+{{\left( -1-3 \right)}^{2}}+{{\left( 1+2 \right)}^{2}}}=\sqrt{34}>R$ nên $A$ nằm ngoài mặt cầu $\left( S \right)$.
Ta lại có $S=AM+4.AN$. Đặt $AM=x$ với $x\in \left[ \sqrt{34}-3; \sqrt{34}+3 \right]$.
Mà $AM.AN=A{{I}^{2}}-{{R}^{2}}=34-9=25$. Suy ra $AN=\dfrac{25}{AM}$.
Do đó $S=f\left( x \right)=x+\dfrac{100}{x}$ với $x\in \left[ \sqrt{34}-3; \sqrt{34}+3 \right]$.
${f}'\left( x \right)=1-\dfrac{100}{{{x}^{2}}}=\dfrac{{{x}^{2}}-100}{{{x}^{2}}}<0$, $\forall x\in \left[ \sqrt{34}-3; \sqrt{34}+3 \right]$.
Do đó $\underset{\left[ \sqrt{34}-3; \sqrt{34}+3 \right]}{\mathop{\min }} f\left( x \right)=f\left( \sqrt{34}+3 \right)=5\sqrt{34}-9$.
Dấu $''=''$ xảy ra $\Leftrightarrow A, M, N, I$ thẳng hàng và $AM=\sqrt{34}+3$ ; $AN=\sqrt{34}-3$.
A. ${{S}_{\min }}=30$.
B. ${{S}_{\min }}=20$.
C. ${{S}_{\min }}=\sqrt{34}-3$.
D. ${{S}_{\min }}=5\sqrt{34}-9$.
Ta có $AI=\sqrt{{{\left( 2-5 \right)}^{2}}+{{\left( -1-3 \right)}^{2}}+{{\left( 1+2 \right)}^{2}}}=\sqrt{34}>R$ nên $A$ nằm ngoài mặt cầu $\left( S \right)$.
Ta lại có $S=AM+4.AN$. Đặt $AM=x$ với $x\in \left[ \sqrt{34}-3; \sqrt{34}+3 \right]$.
Mà $AM.AN=A{{I}^{2}}-{{R}^{2}}=34-9=25$. Suy ra $AN=\dfrac{25}{AM}$.
Do đó $S=f\left( x \right)=x+\dfrac{100}{x}$ với $x\in \left[ \sqrt{34}-3; \sqrt{34}+3 \right]$.
${f}'\left( x \right)=1-\dfrac{100}{{{x}^{2}}}=\dfrac{{{x}^{2}}-100}{{{x}^{2}}}<0$, $\forall x\in \left[ \sqrt{34}-3; \sqrt{34}+3 \right]$.
Do đó $\underset{\left[ \sqrt{34}-3; \sqrt{34}+3 \right]}{\mathop{\min }} f\left( x \right)=f\left( \sqrt{34}+3 \right)=5\sqrt{34}-9$.
Dấu $''=''$ xảy ra $\Leftrightarrow A, M, N, I$ thẳng hàng và $AM=\sqrt{34}+3$ ; $AN=\sqrt{34}-3$.
Đáp án D.