Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau, và...

Phương pháp:
Chuyển khoảng cách từ 2 đường thẳng chéo nhau đến khoảng cách từ đường đến mặt song song, khoảng cách từ điểm đến mặt.
Cách giải:
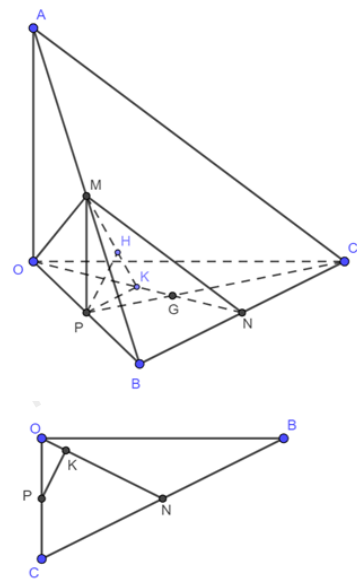Gọi N là trung điểm của BC.
$\Rightarrow MN//AC\Rightarrow AC//\left( OMN \right).$
$\Rightarrow d\left( OM;AC \right)=d\left( AC;\left( OMN \right) \right)=d\left( C;\left( OMN \right) \right).$
Gọi P là trung điểm của OB, G là trọng tâm tam giác OBC.
$\Rightarrow CG=2PG\Rightarrow d\left( C;\left( OMN \right) \right)=2d\left( P;\left( OMN \right) \right)$
Ta có: $\left\{ \begin{aligned}
& MP//OA \\
& OA\bot \left( OBC \right) \\
\end{aligned} \right.\Rightarrow MP\bot \left( OBC \right).$
Kẻ $PK\bot ON,PH\bot MK\Rightarrow PH\bot \left( OMN \right).$
$\Rightarrow d\left( P;\left( OMN \right) \right)=PH.$
Ta có:
${{S}_{PON}}=\dfrac{1}{2}{{S}_{CON}}=\dfrac{1}{4}{{S}_{OBC}}=\dfrac{1}{4}.\dfrac{1}{2}.OB.OC=\dfrac{1}{4}.\dfrac{1}{2}.2a.a=\dfrac{{{a}^{2}}}{4}$.
${{S}_{PON}}=\dfrac{1}{2}.PK.ON=\dfrac{1}{2}.PK.\dfrac{1}{2}BC=\dfrac{1}{2}.PK.\dfrac{1}{2}.a\sqrt{5}=PK.\dfrac{a\sqrt{5}}{4}.$
$\Rightarrow PK.\dfrac{a\sqrt{5}}{4}=\dfrac{{{a}^{2}}}{4}\Rightarrow PK=\dfrac{a\sqrt{5}}{5}.$
Tam giác MPK vuông tại P, PH là đường cao:
$\Rightarrow \dfrac{1}{P{{H}^{2}}}=\dfrac{1}{P{{K}^{2}}}+\dfrac{1}{M{{P}^{2}}}=\dfrac{1}{\dfrac{{{a}^{2}}}{5}}+\dfrac{1}{\dfrac{{{a}^{2}}}{4}}=\dfrac{9}{{{a}^{2}}}\Rightarrow PH=\dfrac{a}{3}.$
$\Rightarrow d\left( OM;AC \right)=2.\dfrac{a}{3}=\dfrac{2a}{3}.$