Gọi $M, N$ lần lượt là điểm biểu diễn của số phức $z$...

Đặt $z=x+yi\left( x,y\in \mathbb{R};x\ge 0 \right)$, ta có
$\left| 2\overline{z}.{{z}^{2}}-4{{\left| z \right|}^{2}} \right|=z.{{\left( \overline{z} \right)}^{2}}+\overline{z}.{{z}^{2}}+4{{\left| z \right|}^{2}}$ $\Leftrightarrow {{\left| z \right|}^{2}}\left| 2z-4 \right|=\left( \bar{z}+z+4 \right){{\left| z \right|}^{2}}$ $\Leftrightarrow \left[ \begin{aligned}
& \left| z \right|=0 \\
& \left| 2z-4 \right|=\left( \bar{z}+z+4 \right) \\
\end{aligned} \right. $ $ \Leftrightarrow \left[ \begin{aligned}
& z=0 \\
& {{\left( x-2 \right)}^{2}}+{{y}^{2}}={{\left( x+2 \right)}^{2}} \\
\end{aligned} \right. $ $ \Leftrightarrow \left[ \begin{aligned}
& z=0 \\
& {{y}^{2}}=8x \\
\end{aligned} \right.$.
Đặt $w=a+bi\left( x,y\in \mathbb{R} \right)$, ta được
$\left| w \right|=\left| \overline{w}+4+2i \right|$ $\Leftrightarrow {{a}^{2}}+{{b}^{2}}={{\left( a+4 \right)}^{2}}+{{\left( b-2 \right)}^{2}}$ $\Leftrightarrow 2a-b+5=0$
Vậy quỹ tích các điểm $N$ là đường thẳng $\Delta :2x-y+5=0$.
Nếu $M\equiv O$ thì khoảng cách $MN$ nhỏ nhất bằng $d\left( O,\Delta \right)=\dfrac{\left| 2.0-0+5 \right|}{\sqrt{5}}=\sqrt{5}$.
Nếu $M$ thuộc parabol ${{y}^{2}}=8x$, ta kẻ tiếp tuyến song song vói $\Delta $ là đường thẳng ${\Delta }':2x-y+1=0$.
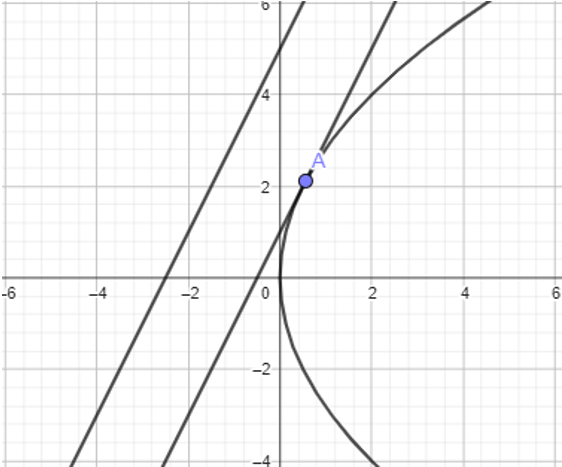thì khoảng cách $MN$ nhỏ nhất bằng $d\left( \Delta ,{\Delta }' \right)=\dfrac{4}{\sqrt{5}}$.
Vậy khoảng cách $MN$ nhỏ nhất bằng $d\left( \Delta ,{\Delta }' \right)=\dfrac{4}{\sqrt{5}}$.