Câu hỏi: Lý thuyết Giá trị lượng giác của góc lượng giác - SGK Toán 11 Kết nối tri thức
a, Khái niệm góc lượng giác và số đo của góc lượng giác
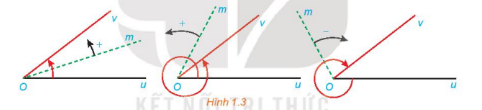
Trong mặt phẳng, cho 2 tia Ou, Ov. Xét tia Om cùng nằm tròn mặt phẳng này. Nếu tia Om quay quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou và tia cuối Ov.
Kí hiệu: (Ou, Ov).
Số đo của góc lượng giác có tia đầu Ou và tia cuối Ov kí hiệu là sđ(Ou, Ov).
b, Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
Sđ(Ou,Ov) + sđ(Ov, Ow) = sđ(Ou,Ow) +k360o.
2. Đơn vị đo góc và độ dài cung tròn
a, Đơn vị đo góc và cung tròn
Đơn vị độ: \({1^o} = 60',1' = 60''\)
Đơn vị rađian: \({1^o} = \frac{\pi }{{180}}\)rad, 1 rad =\({\left( {\frac{{180}}{\pi }} \right)^o}\)
b, Độ dài cung tròn
Một cung tròn của đường tròn bán kính R và có số đo \(\alpha \)rad thì có độ dài \(l = R\alpha \)
3. Giá trị lượng giác của góc lượng giác
a, Đường tròn lượng giác
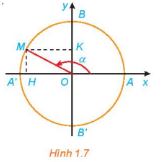
Đường tròn lượng giác là đường tròn có tâm tại gốc tọa độ, bán kính bằng 1, được định hướng và lấy điểm A(1;0) làm điểm gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\alpha \)(độ hoặc rad) là điểm M trên đường tròn lượng giác sao cho sđ (OA, OM) =\(\alpha \).
b, Các giá trị lượng giác của góc lượng giác:
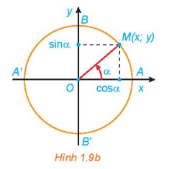
Trục tung là trục sin, trục hoành là trục côsin
Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\).
c, Bảng xác định dấu của các giá trị lượng giác

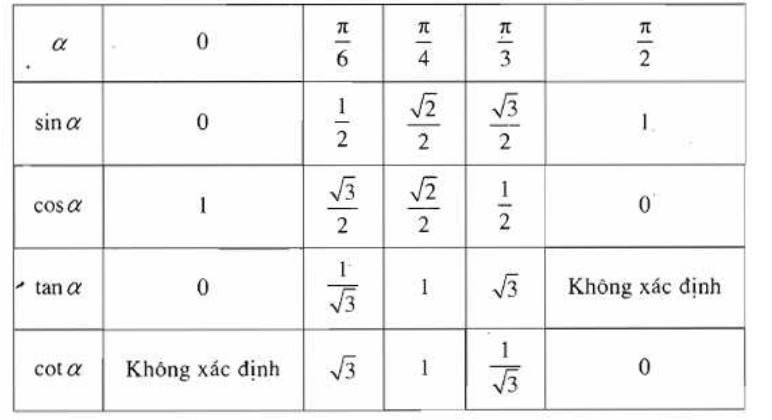
d, Giá trị lượng giác của các góc đặc biệt
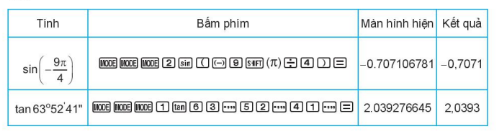
e, Cách bấm máy tính để tìm giá trị lượng giác của góc
4. Quan hệ giữa các giá trị lượng giác
a, Các công thức lượng giác cơ bản
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
b, Giá trị lượng giác của các góc có liên quan đặc biệt (cos đối, sin bù, phụ chéo, khác pi tan)
\(\begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \\\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)
Trong mặt phẳng, cho 2 tia Ou, Ov. Xét tia Om cùng nằm tròn mặt phẳng này. Nếu tia Om quay quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou và tia cuối Ov.
Kí hiệu: (Ou, Ov).
Số đo của góc lượng giác có tia đầu Ou và tia cuối Ov kí hiệu là sđ(Ou, Ov).
b, Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
Sđ(Ou,Ov) + sđ(Ov, Ow) = sđ(Ou,Ow) +k360o.
2. Đơn vị đo góc và độ dài cung tròn
a, Đơn vị đo góc và cung tròn
Đơn vị độ: \({1^o} = 60',1' = 60''\)
Đơn vị rađian: \({1^o} = \frac{\pi }{{180}}\)rad, 1 rad =\({\left( {\frac{{180}}{\pi }} \right)^o}\)
b, Độ dài cung tròn
Một cung tròn của đường tròn bán kính R và có số đo \(\alpha \)rad thì có độ dài \(l = R\alpha \)
3. Giá trị lượng giác của góc lượng giác
a, Đường tròn lượng giác
Đường tròn lượng giác là đường tròn có tâm tại gốc tọa độ, bán kính bằng 1, được định hướng và lấy điểm A(1;0) làm điểm gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\alpha \)(độ hoặc rad) là điểm M trên đường tròn lượng giác sao cho sđ (OA, OM) =\(\alpha \).
b, Các giá trị lượng giác của góc lượng giác:
Trục tung là trục sin, trục hoành là trục côsin
Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\).
c, Bảng xác định dấu của các giá trị lượng giác
d, Giá trị lượng giác của các góc đặc biệt
e, Cách bấm máy tính để tìm giá trị lượng giác của góc
4. Quan hệ giữa các giá trị lượng giác
a, Các công thức lượng giác cơ bản
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
b, Giá trị lượng giác của các góc có liên quan đặc biệt (cos đối, sin bù, phụ chéo, khác pi tan)
\(\begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \\\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)