Google
Câu hỏi: Trong không gian $Oxyz$, cho đường thẳng $d:\dfrac{x-1}{1}=\dfrac{y-1}{3}=\dfrac{z}{2}$ và đường thẳng $\vartriangle :\dfrac{x-2}{1}=\dfrac{y-1}{-1}=\dfrac{z-1}{1}$. Hai mặt phẳng $\left( P \right),\left( Q \right)$ vuông góc với nhau, cùng chứa $d$ và cắt $\vartriangle $ tại $M,N$. Độ dài đoạn thẳng $MN$ ngắn nhất bằng
A. $\dfrac{\sqrt{10}}{10}$.
B. $\dfrac{2\sqrt{10}}{21}$.
C. $\dfrac{\sqrt{5}}{5}$.
D. $\dfrac{\sqrt{42}}{21}$.
A. $\dfrac{\sqrt{10}}{10}$.
B. $\dfrac{2\sqrt{10}}{21}$.
C. $\dfrac{\sqrt{5}}{5}$.
D. $\dfrac{\sqrt{42}}{21}$.
Đường thẳng $d$ đi qua điểm $A\left( 1;1;0 \right)$ và có một vectơ chỉ phương $\overrightarrow{{{u}_{d}}}=\left( 1;3;2 \right)$.
Đường thẳng $\Delta $ đi qua điểm $B\left( 2,1,1 \right)$ và có một vectơ chỉ phương $\overrightarrow{{{u}_{\Delta }}}=\left( 1;-1;1 \right)$.
Ta có: $\overrightarrow{{{u}_{d}}}.\overrightarrow{{{u}_{\Delta }}}=0\Rightarrow d\bot \Delta $.
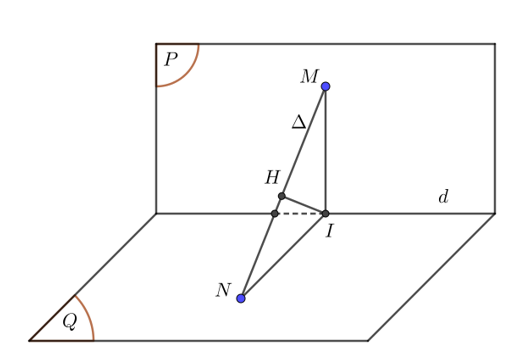Gọi $I$ là hình chiếu của $N$ lên $d$. Do $\left( P \right)\bot \left( Q \right)$ theo giao tuyến $d$ nên $NI\bot \left( P \right)$.
Suy ra $NI\bot MI$ hay $\Delta MIN$ vuông tại $I$.
Gọi $H$ là trung điểm của $MN$, ta có $MN=2IH$.
Do vậy, $MN$ ngắn nhất khi và chỉ khi $IH$ ngắn nhất. Điều đó xảy ra khi và chỉ khi $IH\bot \Delta $.
Ta có $\overrightarrow{AB}\left( 1;0;1 \right)$ và $\left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right]=\left( 5;1;-4 \right)$ nên
$\overrightarrow{AB}.\left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right]=1.5+0.1-1.4=1$ và $\left| \left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right] \right|=\sqrt{{{5}^{2}}+{{1}^{2}}+{{4}^{2}}}=\sqrt{42}$.
Khi đó, $\min IH=d\left( d,\Delta \right)=\dfrac{\left| \overrightarrow{AB}.\left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right] \right|}{\left| \left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right] \right|}=\dfrac{\sqrt{42}}{42}$.
Vậy $\min MN=\dfrac{\sqrt{42}}{21}$.
Đường thẳng $\Delta $ đi qua điểm $B\left( 2,1,1 \right)$ và có một vectơ chỉ phương $\overrightarrow{{{u}_{\Delta }}}=\left( 1;-1;1 \right)$.
Ta có: $\overrightarrow{{{u}_{d}}}.\overrightarrow{{{u}_{\Delta }}}=0\Rightarrow d\bot \Delta $.
Suy ra $NI\bot MI$ hay $\Delta MIN$ vuông tại $I$.
Gọi $H$ là trung điểm của $MN$, ta có $MN=2IH$.
Do vậy, $MN$ ngắn nhất khi và chỉ khi $IH$ ngắn nhất. Điều đó xảy ra khi và chỉ khi $IH\bot \Delta $.
Ta có $\overrightarrow{AB}\left( 1;0;1 \right)$ và $\left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right]=\left( 5;1;-4 \right)$ nên
$\overrightarrow{AB}.\left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right]=1.5+0.1-1.4=1$ và $\left| \left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right] \right|=\sqrt{{{5}^{2}}+{{1}^{2}}+{{4}^{2}}}=\sqrt{42}$.
Khi đó, $\min IH=d\left( d,\Delta \right)=\dfrac{\left| \overrightarrow{AB}.\left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right] \right|}{\left| \left[ \overrightarrow{{{u}_{d}}},\ \overrightarrow{{{u}_{\Delta }}} \right] \right|}=\dfrac{\sqrt{42}}{42}$.
Vậy $\min MN=\dfrac{\sqrt{42}}{21}$.
Đáp án D.