Google
Câu hỏi: Trong không gian $Oxyz$, cho mặt cầu $\left( S \right)$ tâm $I\left( 9;3;1 \right)$, bán kính bằng $3$. Gọi $M,N$ là hai điểm lần lượt thuộc hai trục $Ox,Oz$ sao cho đường thẳng $MN$ tiếp xúc với $\left( S \right)$, đồng thời mặt cầu ngoại tiếp tứ diện $OIMN$ có bán kính bằng $\dfrac{13}{2}$. Gọi $A$ là tiếp điểm của $MN$ và $\left( S \right)$, giá trị $AM.AN$ bằng
A. $12\sqrt{3}$.
B. $18$.
C. $28\sqrt{3}$.
D. $39$.
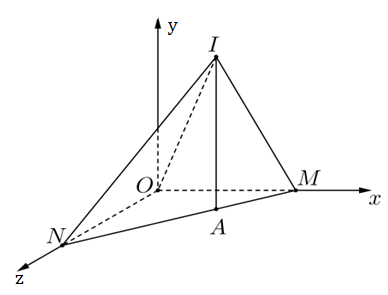Gọi $M\left( a;0;0 \right)\in Ox, N\left( 0;0;b \right)\in Oz$.
Ta có $d\left( I;\left( Oxz \right) \right)=3=R$ nên $\left( S \right)$ tiếp xúc với mặt phẳng $\left( Oxz \right)$ tại điểm $A\left( 9;0;1 \right)$ và $MN$ cũng đi qua $A$.
Lại có $\overrightarrow{AM}=\left( a-9;0;-1 \right), \overrightarrow{AN}=\left( -9;0;b-1 \right)$ và 3 điểm $A,M,N$ thẳng hàng nên ta được: $\dfrac{a-9}{-9}=\dfrac{-1}{b-1}\Leftrightarrow \left( a-9 \right)\left( b-1 \right)=9 \left( 1 \right)$.
Tứ diện $OIMN$ có $IA\bot \left( OMN \right)$ và $\Delta OMN$ vuông tại $O$ nên nếu gọi $J$ là tâm mặt cầu ngoại tiếp tứ diện $OIMN$ thì $J\in \left( IMN \right)$.
Suy ra bán kính mặt cầu ngoại tiếp tứ diện $OIMN$ bằng bán kính đường tròn ngoại tiếp $\Delta IMN$.
Ta có ${{S}_{\Delta IMN}}=\dfrac{IM.IN.MN}{4r}$ (với $r=\dfrac{13}{2}$ bán kính đường tròn ngoại tiếp $\Delta IMN$ ).
$\Leftrightarrow \dfrac{1}{2}IA.MN=\dfrac{IM.IN.MN}{4.\dfrac{13}{2}}\Leftrightarrow IM.IN=13IA\Leftrightarrow IM.IN=39$
$\Leftrightarrow \left[ {{\left( a-9 \right)}^{2}}+10 \right]\left[ {{\left( b-1 \right)}^{2}}+90 \right]=1521 \left( 2 \right)$.
Đặt $\left\{ \begin{aligned}
& m=a-9 \\
& n=b-1 \\
\end{aligned} \right.$.
Từ (1) và (2) ta có hệ $\left\{ \begin{aligned}
& mn=9 \\
& \left( {{m}^{2}}+10 \right)\left( {{n}^{2}}+90 \right)=1521 \\
\end{aligned} \right.$.
Giải hệ ta được: ${{m}^{2}}=3\Rightarrow {{n}^{2}}=27$. Vậy $AM.AN=\sqrt{{{m}^{2}}+1}\sqrt{{{n}^{2}}+81}=12\sqrt{3}$.
A. $12\sqrt{3}$.
B. $18$.
C. $28\sqrt{3}$.
D. $39$.
Ta có $d\left( I;\left( Oxz \right) \right)=3=R$ nên $\left( S \right)$ tiếp xúc với mặt phẳng $\left( Oxz \right)$ tại điểm $A\left( 9;0;1 \right)$ và $MN$ cũng đi qua $A$.
Lại có $\overrightarrow{AM}=\left( a-9;0;-1 \right), \overrightarrow{AN}=\left( -9;0;b-1 \right)$ và 3 điểm $A,M,N$ thẳng hàng nên ta được: $\dfrac{a-9}{-9}=\dfrac{-1}{b-1}\Leftrightarrow \left( a-9 \right)\left( b-1 \right)=9 \left( 1 \right)$.
Tứ diện $OIMN$ có $IA\bot \left( OMN \right)$ và $\Delta OMN$ vuông tại $O$ nên nếu gọi $J$ là tâm mặt cầu ngoại tiếp tứ diện $OIMN$ thì $J\in \left( IMN \right)$.
Suy ra bán kính mặt cầu ngoại tiếp tứ diện $OIMN$ bằng bán kính đường tròn ngoại tiếp $\Delta IMN$.
Ta có ${{S}_{\Delta IMN}}=\dfrac{IM.IN.MN}{4r}$ (với $r=\dfrac{13}{2}$ bán kính đường tròn ngoại tiếp $\Delta IMN$ ).
$\Leftrightarrow \dfrac{1}{2}IA.MN=\dfrac{IM.IN.MN}{4.\dfrac{13}{2}}\Leftrightarrow IM.IN=13IA\Leftrightarrow IM.IN=39$
$\Leftrightarrow \left[ {{\left( a-9 \right)}^{2}}+10 \right]\left[ {{\left( b-1 \right)}^{2}}+90 \right]=1521 \left( 2 \right)$.
Đặt $\left\{ \begin{aligned}
& m=a-9 \\
& n=b-1 \\
\end{aligned} \right.$.
Từ (1) và (2) ta có hệ $\left\{ \begin{aligned}
& mn=9 \\
& \left( {{m}^{2}}+10 \right)\left( {{n}^{2}}+90 \right)=1521 \\
\end{aligned} \right.$.
Giải hệ ta được: ${{m}^{2}}=3\Rightarrow {{n}^{2}}=27$. Vậy $AM.AN=\sqrt{{{m}^{2}}+1}\sqrt{{{n}^{2}}+81}=12\sqrt{3}$.
Đáp án A.