Google
Câu hỏi: Trong không gian ${Oxyz}$, cho mặt cầu ${(S)}$ có tâm ${I\left(1;2;3\right)}$, bán kính ${R=5}$ và điểm ${P\left(2;4;5\right)}$ nằm bên trong mặt cầu. Qua ${P}$ dựng 3 dây cung ${AA'}$, ${BB'}$, ${CC'}$ của mặt cầu ${(S)}$ đôi một vuông góc với nhau. Dựng hình hộp chữ nhật có ba cạnh là ${PA}$, ${PB}$, ${PC}$. Gọi ${PQ}$ là đường chéo của hình hộp chữ nhật đó. Biết rằng ${Q}$ luôn chạy trên một mặt cầu cố định. Bán kính của mặt cầu đó bằng.
A. ${\dfrac{\sqrt{219}}{6}}$.
B. ${\sqrt{61}}$.
C. ${\dfrac{\sqrt{219}}{2}}$.
D. ${\sqrt{57}}$.
A. ${\dfrac{\sqrt{219}}{6}}$.
B. ${\sqrt{61}}$.
C. ${\dfrac{\sqrt{219}}{2}}$.
D. ${\sqrt{57}}$.
CÁCH 1:
Gọi ${G}$ là trọng tâm tam giác ${ABC}$, ta có $3{{R}^{2}}=I{{A}^{2}}+I{{B}^{2}}+I{{C}^{2}}=3I{{G}^{2}}+G{{A}^{2}}+G{{B}^{2}}+G{{C}^{2}}.$ (1)
Lại có $9P{{G}^{2}}=P{{Q}^{2}}=P{{A}^{2}}+P{{B}^{2}}+P{{C}^{2}}=3P{{G}^{2}}+G{{A}^{2}}+G{{B}^{2}}+G{{C}^{2}}.$ (2)
Từ (1) và (2) ta có $3{{R}^{2}}=3I{{G}^{2}}+6P{{G}^{2}}\Leftrightarrow I{{G}^{2}}+2P{{G}^{2}}={{R}^{2}}.$
Vì ${\vec{GQ}+2\vec{GP}=\vec{0}}$ nên ta có
${\begin{aligned}3\vec{IG}&=&\vec{IQ}+2\vec{IP}\\\Rightarrow 9IG^2&=&IQ^2+4IP^2+4 \vec{IQ}\vec{IP}\\&=& IQ^2+4IP^2+2\left(IQ^2+IP^2-PQ^2\right)\\&=&3IQ^2+6IP^2-2PQ^2\\&=&3IQ^2+6IP^2-18PG^2\\\Rightarrow 9IG^2+18PG^2 &=& 3IQ^2+6IP^2\\\Rightarrow 9R^2 &=& 3IQ^2+6IP^2 \\\Rightarrow IQ^2&=&3R^2-2IP^2=57\end{aligned}}$
Vậy điểm ${Q}$ luôn di động trên mặt cầu cố định có tâm ${I}$, bán kính bằng ${\sqrt{57}}$.
CÁCH 2:
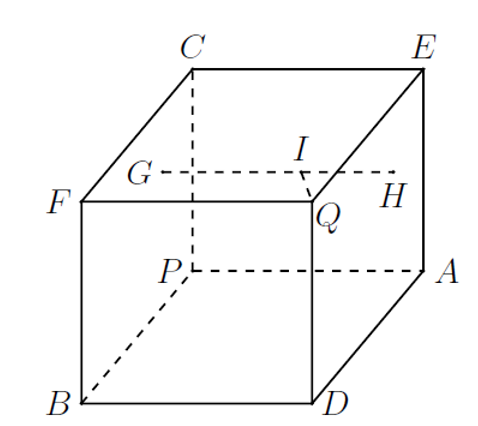Giả sử ta dựng hình hộp chữ nhật ${PADB.CEQF}$ thoả mãn bài toán.
Gọi ${G}$, ${H}$ lần lượt là hình chiếu vuông góc của ${I}$ trên các mặt phẳng ${(PBFC)}$ và ${(ADQE)}$.
Ta có
${\begin{aligned}\vec{IQ}&=&\vec{IA}+\vec{AQ}=\vec{IA}+\vec{PB}+\vec{PC}\\\Rightarrow IQ^2&=&IA^2+PB^2+PC^2+2\vec{IA}\left(\vec{PB}+\vec{PC}\right)+2\vec{PB}\vec{PC}\\&=&R^2+2\vec{HA}\left(\vec{PB}+\vec{PC}\right)+PB^2+PC^2\\&=&R^2+2 \vec{GP}\left(\vec{PB}+\vec{PC}\right)+PB^2+PC^2\\&=&R^2+\left(\vec{GP}+\vec{PB}\right)^2+\left(\vec{GP}+\vec{PC}\right)^2-2GP^2\\&=&R^2+GB^2+GC^2-2GP^2\\&=&R^2+2(R^2-GI^2)-2GP^2\\&=&3R^2-2(GI^2+GP^2)\\&=& 3R^2-2IP^2=57 \\\Rightarrow IQ &=& \sqrt{57}.\end{aligned}}$
Vậy ${Q}$ luôn nằm trên mặt cầu tâm ${I}$, bán kính bằng ${\sqrt{57}}$.
Gọi ${G}$ là trọng tâm tam giác ${ABC}$, ta có $3{{R}^{2}}=I{{A}^{2}}+I{{B}^{2}}+I{{C}^{2}}=3I{{G}^{2}}+G{{A}^{2}}+G{{B}^{2}}+G{{C}^{2}}.$ (1)
Lại có $9P{{G}^{2}}=P{{Q}^{2}}=P{{A}^{2}}+P{{B}^{2}}+P{{C}^{2}}=3P{{G}^{2}}+G{{A}^{2}}+G{{B}^{2}}+G{{C}^{2}}.$ (2)
Từ (1) và (2) ta có $3{{R}^{2}}=3I{{G}^{2}}+6P{{G}^{2}}\Leftrightarrow I{{G}^{2}}+2P{{G}^{2}}={{R}^{2}}.$
Vì ${\vec{GQ}+2\vec{GP}=\vec{0}}$ nên ta có
${\begin{aligned}3\vec{IG}&=&\vec{IQ}+2\vec{IP}\\\Rightarrow 9IG^2&=&IQ^2+4IP^2+4 \vec{IQ}\vec{IP}\\&=& IQ^2+4IP^2+2\left(IQ^2+IP^2-PQ^2\right)\\&=&3IQ^2+6IP^2-2PQ^2\\&=&3IQ^2+6IP^2-18PG^2\\\Rightarrow 9IG^2+18PG^2 &=& 3IQ^2+6IP^2\\\Rightarrow 9R^2 &=& 3IQ^2+6IP^2 \\\Rightarrow IQ^2&=&3R^2-2IP^2=57\end{aligned}}$
Vậy điểm ${Q}$ luôn di động trên mặt cầu cố định có tâm ${I}$, bán kính bằng ${\sqrt{57}}$.
CÁCH 2:
Gọi ${G}$, ${H}$ lần lượt là hình chiếu vuông góc của ${I}$ trên các mặt phẳng ${(PBFC)}$ và ${(ADQE)}$.
Ta có
${\begin{aligned}\vec{IQ}&=&\vec{IA}+\vec{AQ}=\vec{IA}+\vec{PB}+\vec{PC}\\\Rightarrow IQ^2&=&IA^2+PB^2+PC^2+2\vec{IA}\left(\vec{PB}+\vec{PC}\right)+2\vec{PB}\vec{PC}\\&=&R^2+2\vec{HA}\left(\vec{PB}+\vec{PC}\right)+PB^2+PC^2\\&=&R^2+2 \vec{GP}\left(\vec{PB}+\vec{PC}\right)+PB^2+PC^2\\&=&R^2+\left(\vec{GP}+\vec{PB}\right)^2+\left(\vec{GP}+\vec{PC}\right)^2-2GP^2\\&=&R^2+GB^2+GC^2-2GP^2\\&=&R^2+2(R^2-GI^2)-2GP^2\\&=&3R^2-2(GI^2+GP^2)\\&=& 3R^2-2IP^2=57 \\\Rightarrow IQ &=& \sqrt{57}.\end{aligned}}$
Vậy ${Q}$ luôn nằm trên mặt cầu tâm ${I}$, bán kính bằng ${\sqrt{57}}$.
Đáp án D.
