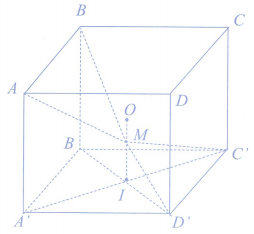
Câu hỏi: Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ có tâm O. Gọi I là tâm của hình vuông ${A}'{B}'{C}'{D}'$ và M là điểm thuộc OI sao cho $MO=\dfrac{1}{2}MI$ (tham khảo hình vẽ). Khi đó, cosin góc tạo bởi hai mặt phẳng $\left( M{C}'{D}' \right)$ và $\left( MAB \right)$ bằng
A. $\dfrac{6\sqrt{13}}{65}$.
B. $\dfrac{7\sqrt{85}}{85}$.
C. $\dfrac{6\sqrt{85}}{85}$.
D. $\dfrac{17\sqrt{13}}{65}$.

A. $\dfrac{6\sqrt{13}}{65}$.
B. $\dfrac{7\sqrt{85}}{85}$.
C. $\dfrac{6\sqrt{85}}{85}$.
D. $\dfrac{17\sqrt{13}}{65}$.
Gọi độ dài cạnh của hình lập phương là a. Hai mặt phẳng $\left( M{C}'{D}' \right)$ và $\left( MAB \right)$ lần lượt chứa hai đường thẳng ${C}'{D}'$, AB mà $AB//{C}'{D}'$ nên giao tuyến của hai mặt phẳng này là đường thẳng qua M và song song với AB. Gọi P, Q lần lượt là trung điểm của ${C}'{D}'$, AB. Các tam giác $\Delta M{C}'{D}'$, $\Delta MAB$ cân ở M nên $MP\bot {C}'{D}'$, $MQ\bot AB$. Do đó nếu $\alpha $ là góc giữa hai mặt phẳng $\left( M{C}'{D}' \right)$ và $\left( MAB \right)$ thì $\cos \alpha =\left| \cos \widehat{PMQ} \right|$ $\left( 1 \right)MQ=\sqrt{M{{I}^{2}}+I{{Q}^{2}}}=\sqrt{{{\left( \dfrac{2}{3}OI \right)}^{2}}+I{{Q}^{2}}}=\sqrt{{{\left( \dfrac{2}{3}.\dfrac{a}{2} \right)}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}}=\dfrac{a\sqrt{13}}{6}$ ; $MP=\dfrac{5a}{6}$ ; $PQ=a\sqrt{2}$
$\cos \alpha =\left| \cos \widehat{PMQ} \right|=\left| \dfrac{M{{P}^{2}}+M{{Q}^{2}}-P{{Q}^{2}}}{2.MP.MQ} \right|=\left| \dfrac{\dfrac{25{{a}^{2}}}{36}+\dfrac{13{{a}^{2}}}{36}-2{{a}^{2}}}{2.\dfrac{5a}{6}.\dfrac{a\sqrt{13}}{6}} \right|=\dfrac{17\sqrt{13}}{65}$
$\cos \alpha =\left| \cos \widehat{PMQ} \right|=\left| \dfrac{M{{P}^{2}}+M{{Q}^{2}}-P{{Q}^{2}}}{2.MP.MQ} \right|=\left| \dfrac{\dfrac{25{{a}^{2}}}{36}+\dfrac{13{{a}^{2}}}{36}-2{{a}^{2}}}{2.\dfrac{5a}{6}.\dfrac{a\sqrt{13}}{6}} \right|=\dfrac{17\sqrt{13}}{65}$
Đáp án D.