Google
Câu hỏi: Trong không gian $O x y z$, cho mặt cầu $(S):(x-1)^2+(y+2)^2+(z-3)^2=27$. Gọi $(\alpha)$ là mặt phẳng đi qua hai điểm $A(0 ; 0 ;-4), B(2 ; 0 ; 0)$ và cắt $(S)$ theo giao tuyến là đường tròn $(C)$ sao cho khối nón đỉnh là tâm của $(S)$ và đáy là đường tròn có thể tích lớn nhất. Biết rằng $(\alpha): a x+b y-z+$ $c=0$, khi đó $a-b+c$ bằng
A. -4 .
B. 8 .
C. 0 .
D. 2 .
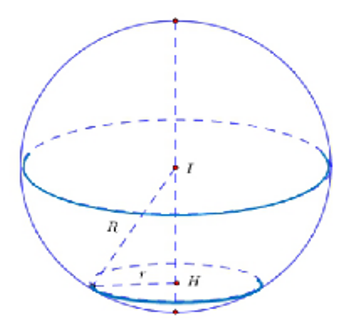Mặt cầu $(S)$ có tâm $I(1 ;-2 ; 3)$ và bán kính $R=3 \sqrt{3}$.
Vì $(\alpha): a x+b y-z+c=0$ đi qua hai điểm $A(0 ; 0 ;-4), B(2 ; 0 ; 0)$ nên $c=-4$ và $a=2$.
Suy ra $(\alpha): 2 x+b y-z-4=0$
Đặt $I H=x$, với $0<x<3 \sqrt{3}$ ta có $r=\sqrt{R^2-x^2}=\sqrt{27-x^2}$.
Thể tích khối nón là $V=\dfrac{1}{3} \pi r^2 \cdot I H=\dfrac{1}{3} \pi\left(27-x^2\right) \cdot x=\dfrac{1}{3 \sqrt{2}} \pi \sqrt{\left(27-x^2\right) \cdot\left(27-x^2\right) \cdot 2 x^2} \leq$
$18 \pi$
$V_{\max }=18 \pi$ khi $27-x^2=2 x^2 \Leftrightarrow x=3$
Khi đó, $d(I ;(\alpha))=\dfrac{|2 b+5|}{\sqrt{b^2+5}}=3 \Leftrightarrow(2 b+5)^2=9\left(b^2+5\right) \Leftrightarrow b=2$.
Vậy $a-b+c=-4$.
A. -4 .
B. 8 .
C. 0 .
D. 2 .
Vì $(\alpha): a x+b y-z+c=0$ đi qua hai điểm $A(0 ; 0 ;-4), B(2 ; 0 ; 0)$ nên $c=-4$ và $a=2$.
Suy ra $(\alpha): 2 x+b y-z-4=0$
Đặt $I H=x$, với $0<x<3 \sqrt{3}$ ta có $r=\sqrt{R^2-x^2}=\sqrt{27-x^2}$.
Thể tích khối nón là $V=\dfrac{1}{3} \pi r^2 \cdot I H=\dfrac{1}{3} \pi\left(27-x^2\right) \cdot x=\dfrac{1}{3 \sqrt{2}} \pi \sqrt{\left(27-x^2\right) \cdot\left(27-x^2\right) \cdot 2 x^2} \leq$
$18 \pi$
$V_{\max }=18 \pi$ khi $27-x^2=2 x^2 \Leftrightarrow x=3$
Khi đó, $d(I ;(\alpha))=\dfrac{|2 b+5|}{\sqrt{b^2+5}}=3 \Leftrightarrow(2 b+5)^2=9\left(b^2+5\right) \Leftrightarrow b=2$.
Vậy $a-b+c=-4$.
Đáp án A.