Google
Câu hỏi: Trong không gian với hệ tọa độ $O x y z$, cho mặt cầu $(S):(x-1)^2+y^2+(z+2)^2=4$ và đường thẳng $d:\left\{\begin{array}{l}x=2-t \\ y=t \\ z=m-1+t\end{array}\right.$. Gọi $T$ là tập tất cả các giá trị của $m$ để $d$ cắt $(S)$ tại hai điểm phân biệt $A$, $B$ sao cho các tiếp diện của $(S)$ tại $A$ và $B$ tạo với nhau góc lớn nhất có thể. Tính tổng các phần tử của tập hợp $T$.
A. 3 .
B. -3 .
C. -5 .
D. -4 .
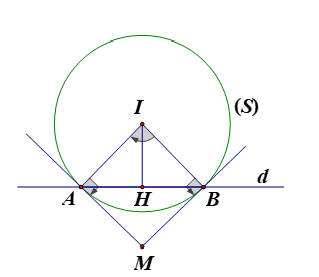Mặt cầu $(S)$ có tâm $I(1 ; 0 ;-2)$ và bán kính $R=2$.
Đường thẳng $d$ đi qua điểm $N(2 ; 0 ; m-1)$ và có véc tơ chỉ phương $\vec{u}=(-1 ; 1 ; 1)$.
Điều kiện để $d$ cắt $(S)$ tại hai điểm phân biệt là $d(I ;(d))<R \Leftrightarrow \dfrac{|[I N ; \vec{u}]|}{|\vec{u}|}<2$
$\Leftrightarrow \dfrac{\sqrt{2 m^2+6 m+6}}{\sqrt{3}}<2 \Leftrightarrow \dfrac{-3-\sqrt{21}}{2}<m<\dfrac{-3+\sqrt{21}}{2}$.
Khi đó, tiếp diện của $(S)$ tại $A$ và $B$ vuông góc với $I A$ và $I B$ nên góc giữa chúng là góc $(I A ; I B)$.
Ta có $0^{\circ} \leq(I A ; I B) \leq 90^{\circ}$ nên $(I A ; I B)_{\max }=90^{\circ} \Leftrightarrow I A \perp I B$.
Từ đó suy ra $d(I ;(d))=\dfrac{1}{2} A B=\sqrt{2} \Leftrightarrow \dfrac{\sqrt{2 m^2+6 m+6}}{\sqrt{3}}=\sqrt{2} \Leftrightarrow 2 m^2+6 m=0 \Leftrightarrow\left[\begin{array}{l}m=0 \\ m=-3\end{array}\right.$ (thỏa).
Vậy $T=\{-3 ; 0\}$. Tổng các phần tử của tập hợp $T$ bằng -3 .
A. 3 .
B. -3 .
C. -5 .
D. -4 .
Đường thẳng $d$ đi qua điểm $N(2 ; 0 ; m-1)$ và có véc tơ chỉ phương $\vec{u}=(-1 ; 1 ; 1)$.
Điều kiện để $d$ cắt $(S)$ tại hai điểm phân biệt là $d(I ;(d))<R \Leftrightarrow \dfrac{|[I N ; \vec{u}]|}{|\vec{u}|}<2$
$\Leftrightarrow \dfrac{\sqrt{2 m^2+6 m+6}}{\sqrt{3}}<2 \Leftrightarrow \dfrac{-3-\sqrt{21}}{2}<m<\dfrac{-3+\sqrt{21}}{2}$.
Khi đó, tiếp diện của $(S)$ tại $A$ và $B$ vuông góc với $I A$ và $I B$ nên góc giữa chúng là góc $(I A ; I B)$.
Ta có $0^{\circ} \leq(I A ; I B) \leq 90^{\circ}$ nên $(I A ; I B)_{\max }=90^{\circ} \Leftrightarrow I A \perp I B$.
Từ đó suy ra $d(I ;(d))=\dfrac{1}{2} A B=\sqrt{2} \Leftrightarrow \dfrac{\sqrt{2 m^2+6 m+6}}{\sqrt{3}}=\sqrt{2} \Leftrightarrow 2 m^2+6 m=0 \Leftrightarrow\left[\begin{array}{l}m=0 \\ m=-3\end{array}\right.$ (thỏa).
Vậy $T=\{-3 ; 0\}$. Tổng các phần tử của tập hợp $T$ bằng -3 .
Đáp án B.