Google
Câu hỏi: Trong không gian với hệ trục tọa độ $O x y z$, cho hai điểm $A(2 ; 1 ; 3), B(6 ; 5 ; 5)$. Gọi $(S)$ là mặt cầu có đường kính $A B$. Mặt phẳng $(P)$ vuông góc với đoạn $A B$ tại $H$ sao cho khối nón đỉnh $A$ và đáy là hình tròn tâm $H$ (giao của mặt cầu $(S)$ và mặt phẳng $(P)$ ) có thể tích lớn nhất, biết rằng $(P): 2 x+$ $b y+c z+d=0$ với $b, c, d \in \mathbb{Z}$. Tính $S=b+c+d$.
A. $S=-14$.
B. $S=-18$.
C. $S=-11$.
D. $S=-24$.
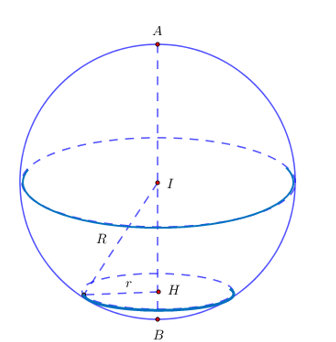Ta có $\overrightarrow{A B}=(4 ; 4 ; 2) \Rightarrow A B=6$ suy ra mặt cầu $(S)$ có tâm $I(4 ; 3 ; 4)$ và bán kính $R=3$.
Đặt $I H=x(0 \leq x \leq 3)$.
Gọi $r$ là bán kính đường tròn tâm $H$ suy ra $r=\sqrt{R^2-x^2}=\sqrt{9-x^2}$.
Thể tích khối nón là $V=\dfrac{1}{3} \pi r^2$. $A H=\dfrac{1}{3} \pi \cdot\left(3^2-x^2\right) \cdot(3+x)$.
Áp dụng bất đẳng thức Cô si ta có $V=\dfrac{1}{6} \pi(6-2 x)(3+x)(3+x) \leq \dfrac{1}{6} \pi\left(\dfrac{6+3+3}{3}\right)^3 \Leftrightarrow V \leq \dfrac{32 \pi}{3}$.
Vậy thể tích khối nón lớn nhất bằng $\dfrac{32 \pi}{3}$ khi $6-x=3+x \Leftrightarrow x=\dfrac{3}{2} \Leftrightarrow I H=\dfrac{3}{2}$.
Mặt phẳng $(P)$ vó vec tơ pháp tuyến $\vec{n}=(2 ; b ; c)$. Vì $(P)$ vuông góc với đoạn $A B$ nên ta có $\vec{n}$ cùng phương với $\overrightarrow{A B} \Leftrightarrow \dfrac{2}{4}=\dfrac{b}{4}=\dfrac{c}{2} \Leftrightarrow\left\{\begin{array}{l}b=2 \\ c=1\end{array}\right.$. Vậy $(P): 2 x+2 y+z+d=0$.
Mặt khác $d(I ;(P))=1 \Leftrightarrow \dfrac{|8+6+4+d|}{\sqrt{2^2+2^2+1}}=1 \Leftrightarrow|18+d|=3 \Leftrightarrow\left[\begin{array}{l}18+d=3 \\ 18+d=-3\end{array} \Leftrightarrow\left[\begin{array}{l}d=-15 \\ d=-21\end{array}\right.\right.$.
Mặt khác $A$ và $I$ nằm cùng phía với mặt phẳng $(P)$ nên ta có $(9+d)(18+d)>0 \Leftrightarrow\left[\begin{array}{l}d<-18 \\ d>-9\end{array}\right.$.
Vậy $d=-21$ suy ra $S=b+c+d=2+1-21=-18$.
A. $S=-14$.
B. $S=-18$.
C. $S=-11$.
D. $S=-24$.
Đặt $I H=x(0 \leq x \leq 3)$.
Gọi $r$ là bán kính đường tròn tâm $H$ suy ra $r=\sqrt{R^2-x^2}=\sqrt{9-x^2}$.
Thể tích khối nón là $V=\dfrac{1}{3} \pi r^2$. $A H=\dfrac{1}{3} \pi \cdot\left(3^2-x^2\right) \cdot(3+x)$.
Áp dụng bất đẳng thức Cô si ta có $V=\dfrac{1}{6} \pi(6-2 x)(3+x)(3+x) \leq \dfrac{1}{6} \pi\left(\dfrac{6+3+3}{3}\right)^3 \Leftrightarrow V \leq \dfrac{32 \pi}{3}$.
Vậy thể tích khối nón lớn nhất bằng $\dfrac{32 \pi}{3}$ khi $6-x=3+x \Leftrightarrow x=\dfrac{3}{2} \Leftrightarrow I H=\dfrac{3}{2}$.
Mặt phẳng $(P)$ vó vec tơ pháp tuyến $\vec{n}=(2 ; b ; c)$. Vì $(P)$ vuông góc với đoạn $A B$ nên ta có $\vec{n}$ cùng phương với $\overrightarrow{A B} \Leftrightarrow \dfrac{2}{4}=\dfrac{b}{4}=\dfrac{c}{2} \Leftrightarrow\left\{\begin{array}{l}b=2 \\ c=1\end{array}\right.$. Vậy $(P): 2 x+2 y+z+d=0$.
Mặt khác $d(I ;(P))=1 \Leftrightarrow \dfrac{|8+6+4+d|}{\sqrt{2^2+2^2+1}}=1 \Leftrightarrow|18+d|=3 \Leftrightarrow\left[\begin{array}{l}18+d=3 \\ 18+d=-3\end{array} \Leftrightarrow\left[\begin{array}{l}d=-15 \\ d=-21\end{array}\right.\right.$.
Mặt khác $A$ và $I$ nằm cùng phía với mặt phẳng $(P)$ nên ta có $(9+d)(18+d)>0 \Leftrightarrow\left[\begin{array}{l}d<-18 \\ d>-9\end{array}\right.$.
Vậy $d=-21$ suy ra $S=b+c+d=2+1-21=-18$.
Đáp án B.