Google
Câu hỏi: Gọi $S$ là tập hợp các số phức $z=a+bi\left( a,b\in \mathbb{R} \right)$ thỏa mãn $\left| z+\overline{z} \right|+\left| z-\overline{z} \right|=2$ và $ab\le 0.$ Xét ${{z}_{1}}$ và ${{z}_{2}}$ thuộc $S$ sao cho $\dfrac{{{z}_{1}}-{{z}_{2}}}{-1+i}$ là số thực dương. Giá trị nhỏ nhất của biểu thức $\left| {{z}_{1}} \right|+\left| {{z}_{2}}-i \right|$ bằng:
A. $\sqrt{5}$.
B. $1+\sqrt{2}$.
C. $1$.
D. $\sqrt{2}$.
A. $\sqrt{5}$.
B. $1+\sqrt{2}$.
C. $1$.
D. $\sqrt{2}$.
Ta có $z=a+bi\left( a,b\in \mathbb{R} \right)$.
Khi đó $\left| z+\overline{z} \right|+\left| z-\overline{z} \right|=2\Leftrightarrow 2\left| a \right|+2\left| b \right|=2\Leftrightarrow \left| a \right|+\left| b \right|=1,ab\le 0.$
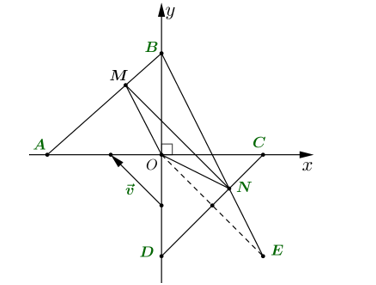Do $ab\le 0.$ nên tập hợp các điểm biểu diễn số phức $z=a+bi\left( a,b\in \mathbb{R} \right)$ là hai cạnh hình vuông $ABCD$ với $A\left( -1 ; 0 \right), B\left( 0 ; 1 \right), C\left( 1 ; 0 \right), D\left( 0 ; -1 \right)$
Gọi $M\left( {{z}_{1}} \right), N\left( {{z}_{2}} \right)$ ta có: $\dfrac{{{z}_{1}}-{{z}_{2}}}{-1+i}=k , \left( k>0 \right) \Rightarrow \overrightarrow{MN}=k\overrightarrow{v}$ với $\overrightarrow{v}=\left( -1;1 \right)$
nên $\overrightarrow{MN}$ cùng hướng với $\overrightarrow{v} \Rightarrow MN \text{//} AD \text{//} BC$
Gọi $E\left( 1 ;-1 \right)$ là điểm đối xứng với $O$ qua đoạn thẳng $CD$
Suy ra $P=\left| {{z}_{1}} \right|+\left| {{z}_{2}}-i \right|=MO+NB=NO+NB=NE+NB\ge BE=\sqrt{5}$
Dấu bằng xảy ra khi và chỉ khi $N\equiv {{N}_{0}}=BE\cap CD.$
Vậy ${{P}_{\min }}=\sqrt{5}$ khi $E ; N ; B$ thẳng hàng.
Khi đó $\left| z+\overline{z} \right|+\left| z-\overline{z} \right|=2\Leftrightarrow 2\left| a \right|+2\left| b \right|=2\Leftrightarrow \left| a \right|+\left| b \right|=1,ab\le 0.$
Gọi $M\left( {{z}_{1}} \right), N\left( {{z}_{2}} \right)$ ta có: $\dfrac{{{z}_{1}}-{{z}_{2}}}{-1+i}=k , \left( k>0 \right) \Rightarrow \overrightarrow{MN}=k\overrightarrow{v}$ với $\overrightarrow{v}=\left( -1;1 \right)$
nên $\overrightarrow{MN}$ cùng hướng với $\overrightarrow{v} \Rightarrow MN \text{//} AD \text{//} BC$
Gọi $E\left( 1 ;-1 \right)$ là điểm đối xứng với $O$ qua đoạn thẳng $CD$
Suy ra $P=\left| {{z}_{1}} \right|+\left| {{z}_{2}}-i \right|=MO+NB=NO+NB=NE+NB\ge BE=\sqrt{5}$
Dấu bằng xảy ra khi và chỉ khi $N\equiv {{N}_{0}}=BE\cap CD.$
Vậy ${{P}_{\min }}=\sqrt{5}$ khi $E ; N ; B$ thẳng hàng.
Đáp án A.